题目内容

16．已知随机变量ξ的数学期望为Eξ，方差为Dξ，随机变量n=$\frac{ξ-Eξ}{\sqrt{Dξ}}$，则Dn的值为1．

分析 由已知条件推导出En=0，从而得到Dn=$\frac{Dξ}{（\sqrt{Dξ}）^{2}}$=1．

解答 解：∵随机变量ξ的数学期望为Eξ，方差为Dξ，随机变量n=$\frac{ξ-Eξ}{\sqrt{Dξ}}$，
∴En=E（$\frac{ξ-Eξ}{\sqrt{Dξ}}$）=$\frac{Eξ-Eξ}{\sqrt{Dξ}}$=0，
∴Dn=$\frac{Dξ}{（\sqrt{Dξ}）^{2}}$=1．
故答案为：1．

点评 本题考查离散型随机变量的方差的求法，是基础题，解题时要认真审题，注意数学期望和方差的性质的合理运用．

练习册系列答案
相关题目
20．假设老鼠每月生子一次．每次生12只，均雌雄各半，小鼠下月又生小鼠，现在有雌雄两只老鼠，在1月生小鼠12只，2月亲代和子代每对又生12只，此后每月，子又生孙，孙又生子，那么到12月份，你能算出总共有多少只老鼠吗？
7．O为平面上一定点，A、B、C是平面上不共线的三点．
（1）若$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ（$\overrightarrow{AB}$+$\overrightarrow{AC}$），λ∈[0，+∞），则P的轨迹一定过△ABC的重心．
（2）若$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ（$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$），λ∈[0，+∞），则P的轨迹一定过△ABC的内心．
（3）若$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ（$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|sinB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|sinC}$），λ∈[0，+∞），则P的轨迹一定过△ABC的重心．
（4）若$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ（$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|cosB}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|cosC}$），λ∈[0，+∞），则P的轨迹一定过△ABC的垂心．
4．某校为了选拔学生参加体育比赛，对5名学生的体能和心理进行了测评，成绩（单位：分）如下表：
学生编号i 1 2 3 4 5 
 体能成绩x80 75 70 65 60 
 心理成绩y 7066 68 64 62 
（1）在本次测评中，规定体能成绩70分以上（含70分）且心理成绩65分以上（含65分）为优秀成绩，从这5名学生中任意抽取2名学生，设X表示成绩优秀的学生人数，求X的分布列和数学期望；
（2）假设学生的体能成绩和心理成绩具有线性相关关系，根据上表利用最小二乘法，求y与x的回归直线方程，（参考数据：$\underset{\stackrel{5}{∑}}{i=1}$xiyi=23190，$\underset{\stackrel{5}{∑}}{i=1}$xi2=24750）．
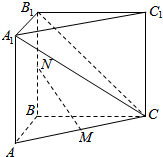11．如图在三棱柱ABC-A1B1C1中，AB=BC=2，AC=2$\sqrt{2}$，侧面ABB1A1是矩形，M，N分别是AC，BB1的中点．
（1）证明：MN∥面A1B1C；
（2）证明：面A1B1C⊥面BCC1B1．
1．在极坐标系中，极点为O，已知P1（1+$\sqrt{2}$，0），P2（1+$\sqrt{2}$，$\frac{π}{2}$），曲线C：p=2$\sqrt{2}$sinθ．
（1）求直线P1P2的极坐标方程；
（2）记直线P1P2与曲线C交与A，B两点，求∠AOB的大小．
8．已知函数f（x）=lnx，g（x）=mx-1．
（1）若f（x）≤g（x）恒成立，求m的取值范围；
（2）若n∈N*且n＞1，求证：$\frac{3}{{2}^{2}}$+$\frac{5}{{3}^{2}}$+…+$\frac{2n-1}{{n}^{2}}$＜2lnn．
5．求与圆：（x+1）2+y2=1，外切且与y轴相切的动圆的圆心轨迹方程．
6．设Sn是正项数列{an}的前n项和，且Sn=$\frac{1}{2}$an2+$\frac{1}{2}$an-1（n∈N*）
（1）设数列{an}的通项公式；
（2）若bn=2n，设cn=anbn，求数列{cn}的前n项和Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网