题目内容
如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中,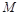 是
是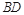 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.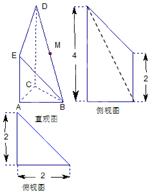
(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求出该几何体的体积.
(1)详见解析;(2)4
解析试题分析:(1)要证明直线和平面平行,只需证明直线和平面内的一条直线平行即可,该题取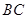 中点
中点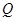 ,连
,连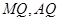 ,先证
,先证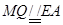 ,则四边形
,则四边形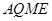 是平行四边形,从而
是平行四边形,从而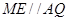 ,进而证明
,进而证明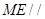 面
面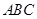 ;
;
(2)该几何体可以看作是以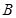 为顶点,四边形
为顶点,四边形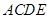 为底面的四棱锥,直棱柱中
为底面的四棱锥,直棱柱中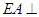 平面
平面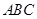 ,所以
,所以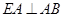 ,又由俯视图可知
,又由俯视图可知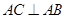 ,故可证明
,故可证明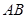
 面
面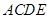 ,所以四棱锥的高为
,所以四棱锥的高为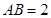 ,再求底面
,再求底面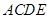 的面积,进而求该几何体的体积.
的面积,进而求该几何体的体积.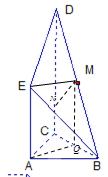
试题解析:(Ⅰ)取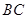 中点
中点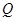 ,连
,连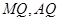
 ,又因为
,又因为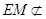 面
面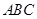 ,而
,而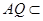 面
面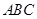 ,所以
,所以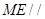 面
面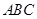 ;
;
(Ⅱ)由俯视图知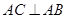 ①且
①且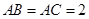 ,直棱柱中
,直棱柱中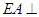 平面
平面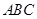 ,所以
,所以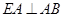 ②
②
由①②知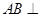 平面
平面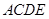 ,所以
,所以 是棱锥
是棱锥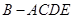 的高.
的高.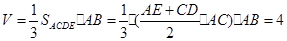
考点:1、三视图;2、直线和平面平行的判定;3、几何体的体积.

练习册系列答案
相关题目
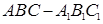 中,
中,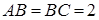 ,
,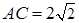 ,
,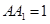 ,D为BC的中点.
,D为BC的中点.
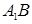 ∥面
∥面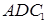 ;
; 的体积.
的体积. 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.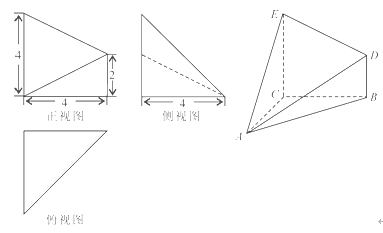
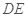 与
与 所成角的余弦值;
所成角的余弦值;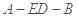 的正弦值;
的正弦值; 
 与
与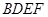 均为菱形,设
均为菱形,设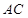 与
与 相交于点
相交于点 ,若
,若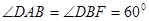 ,且
,且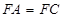 .
.
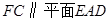 ;
;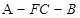 的余弦值.
的余弦值.
 中,
中,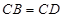 ,
,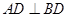 ,点
,点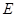 ,
,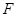 分别是
分别是 ,
, 的中点.
的中点.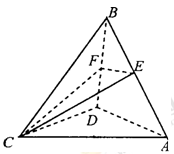
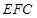 ⊥平面
⊥平面 ;
; ⊥平面
⊥平面 ,求三棱锥
,求三棱锥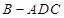 的体积.
的体积.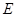 是矩形
是矩形 中
中 边上的点,
边上的点, 为
为 边的中点,
边的中点,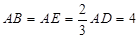 ,现将
,现将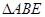 沿
沿 边折至
边折至 位置,且平面
位置,且平面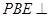 平面
平面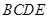 .
.  ;
;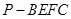 的体积.
的体积. 
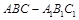 中,侧面
中,侧面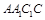 是边长为2的正方形,
是边长为2的正方形,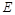 是
是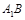 的中点,
的中点,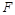 在棱
在棱 上.
上.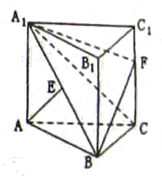
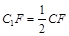 时,求三棱锥
时,求三棱锥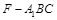 的体积.
的体积.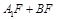 最小时,判断直线
最小时,判断直线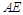 与
与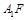 是否垂直,并证明结论.
是否垂直,并证明结论.