题目内容
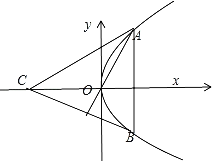
【题目】过抛物线y2＝4x焦点F的直线交该抛物线于A,B两点,且|AB|＝4,若原点O是△ABC的垂心,则点C的坐标为_____．
【答案】
【解析】
由题意设直线AB的方程,与抛物线联立求出两根之和,由抛物线的性质可得弦长|AB|的表达式,再由题意可得参数的值,进而求出直线的方程,代入抛物线的方程求出A,B的坐标,由O为三角形ABC的垂心可得C在x轴上,设C的坐标,由OA⊥BC,可得数量积为0,求出C点的坐标．
解：显然直线AB的斜率不为0,
由题意设直线AB的方程为：x＝my+1,设A（x1,y1）,B（x2,y2）,
联立直线AB与抛物线的方程
,
整理可得y2﹣4my﹣4＝0,y1+y2＝4m,所以x1+x2＝4m2+2,
由抛物线的性质可得|AB|＝x1+x2+2＝4m2+4,
由题意可得4m2+4＝4,所以m＝0,即直线AB垂直于x轴,
所以可得A（1,2）,B（1,﹣2）,
因为原点O是△ABC的垂心,所以C在x轴上,设C（a,0）,可得AO⊥BC,即
0
即（1,2）（1﹣a,﹣2）＝0,整理可得：1﹣a﹣4＝0,解得a＝﹣3,
所以C的坐标为：,
故答案为：．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
