题目内容
2.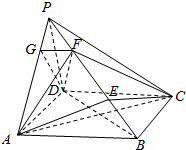 已知四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2$\sqrt{2}$的正方形,PD=4,E,F是PB上的动点,且EF=2.
已知四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2$\sqrt{2}$的正方形,PD=4,E,F是PB上的动点,且EF=2.(1)求证:AC⊥平面PDB;
(2)求三棱锥F-AEC的体积;
(3)若点G在PA上运动,且满足$\frac{PG}{PA}$=$\frac{PF}{PB}$=x,试将三棱锥A-DGF的体积V表示为x的函数,并求体积V的最大值.
分析 (1)由已知结合线面垂直的判断得答案;
(2)把三棱锥F-AEC的体积转化为以OEF为底面,分别以OA、OC为高的两个三棱锥的体积求解;
(3)由平行线截线段成比例定理,把三棱锥A-DGF(F-ADG)的底面ADG的高及棱锥的高GF用含x的代数式表示,代入三棱锥体积公式,化为关于x的函数,由二次函数求得最大值.
解答  (1)证明:∵四边形ABCD是正方形,∴AC⊥BD,
(1)证明:∵四边形ABCD是正方形,∴AC⊥BD,
∵PD⊥平面ABCD,AC?平面ABCD,∴AC⊥PD,
又PD∩BD=D,∴AC⊥平面PDB;
(2)解:∵四边形ABCD是边长为2$\sqrt{2}$的正方形,∴BD=4,
又PD=4,∴D到PB的距离为$2\sqrt{2}$,
设AC∩BD=O,则O到PB的距离为$\sqrt{2}$.
连接OE,OF,∴${S}_{△OEF}=\frac{1}{2}×2×\sqrt{2}=\sqrt{2}$.
∴${V}_{F-AEC}=\frac{1}{3}×\sqrt{2}×4=\frac{4\sqrt{2}}{3}$;
(3)解:∵$\frac{PG}{PA}$=$\frac{PF}{PB}$=x,∴$\frac{GF}{AB}=\frac{GF}{2\sqrt{2}}=x$,
∴$GF=2\sqrt{2}x$.
设G到AD的距离为h,由平行线截线段成比例定理可得:$\frac{4-h}{4}=x$,
∴h=4-4x,
∴${S}_{△ADG}=\frac{1}{2}×2\sqrt{2}×(4-4x)=4\sqrt{2}(1-x)$,
∴三棱锥A-DGF的体积V=$\frac{1}{3}•{S}_{△ADG}•FG$=$\frac{1}{3}•4\sqrt{2}(1-x)•2\sqrt{2}x$=$\frac{16}{3}(-{x}^{2}+x)$.
∵PB=$4\sqrt{2}$,EF=2,∴0$<x<\frac{4\sqrt{2}-2}{4\sqrt{2}}$=$1-\frac{\sqrt{2}}{4}$.
则$V=\frac{16}{3}(-{x}^{2}+x)$,0$<x<1-\frac{\sqrt{2}}{4}$.
∴当x=$\frac{1}{2}$时,V取得最大值为$\frac{4}{3}$.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案| A. | 抛物线 | B. | 双曲线 | C. | 直线 | D. | 圆 |
| 车尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(1)若p=0.8,求汽车A在同一周内恰有两天连续出车的概率;
(2)若p∈[0.4,0.8],且两车的日出车频率之和为1,为实现节能减排与绿色出行,应如何调控两车的日出车频率,使得一周内汽车A,B同日都出车的平均天数最少.
 如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.
如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.