题目内容
12.给定函数①y=x${\;}^{\frac{1}{2}}$,②y=log${\;}_{\frac{1}{2}}$(x+1),③y=|x-1|,④y=2x+1,⑤f(x)=$\frac{{4}^{x}+1}{{2}^{x}}$其中在区间(0,1)上单调递减的函数序号是②③.分析 由函数图象,对数函数的单调性,一次函数的单调性,指数函数的单调性,以及函数导数符号和函数单调性的关系即可判断每个函数在(0,1)上的单调性,从而得出在(0,1)上为减函数的序号.
解答 解:①根据函数$y={x}^{\frac{1}{2}}$的图象即知该函数在(0,1)上单调递增;
②由对数函数的单调性知函数$y=lo{g}_{\frac{1}{2}}(x+1)$在(0,1)上单调递减;
③x∈(0,1),∴y=|x-1|=-x+1,该一次函数在(0,1)上显然是减函数;
④根据指数函数的单调性知函数y=2x+1在(0,1)上为增函数;
⑤f′(x)=$\frac{{2}^{x}ln2({4}^{x}-1)}{{4}^{x}}$;
∵x>0;
∴4x-1>0;
∴f′(x)>0;
∴函数f(x)在(0,1)上单调递增;
∴在(0,1)上单调递减的函数序号为:②③.
故答案为:②③.
点评 考查对函数$y={x}^{\frac{1}{2}}$图象的掌握,对数函数和指数函数,及一次函数的单调性,含绝对值函数的处理方法:去绝对值号,以及函数导数符号和函数单调性的关系,注意正确求导.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
17.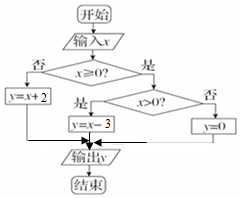 执行如图所示的程序框图,若从集合A={x|-10≤x≤10}中随机取一个数输入,则输出的y值落在区间(-5,2)内的概率是( )
执行如图所示的程序框图,若从集合A={x|-10≤x≤10}中随机取一个数输入,则输出的y值落在区间(-5,2)内的概率是( )
 执行如图所示的程序框图,若从集合A={x|-10≤x≤10}中随机取一个数输入,则输出的y值落在区间(-5,2)内的概率是( )
执行如图所示的程序框图,若从集合A={x|-10≤x≤10}中随机取一个数输入,则输出的y值落在区间(-5,2)内的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.某鱼类养殖户在一个鱼池中养殖一种鱼,每季养殖成本为10000元,此鱼的市场价格和鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
(Ⅰ)设X表示在这个鱼池养殖1季这种鱼的利润,求X的分布列和期望;
(Ⅱ)若在这个鱼池中连续3季养殖这种鱼,求这3季中至少有2季的利润不少于20000元的概率.
| 鱼池产量(kg) | 300 | 500 |
| 概 率 | 0.5 | 0.5 |
| 鱼的市场价格(元/(kg) | 60 | 100 |
| 概 率 | 0.4 | 0.6 |
(Ⅱ)若在这个鱼池中连续3季养殖这种鱼,求这3季中至少有2季的利润不少于20000元的概率.