题目内容
12.已知:a,b∈R+,且a≠b,求证:a3+b3>a2b+ab2.分析 法一,分析法:证明使a3+b3>a2b+ab2成立的充分条件成立.
法二,综合法:由条件a≠b推出:a2-2ab+b2>0,通过变形,应用不等式的性质可证出结论.
解答 证明:法一:(分析法)a3+b3>a2b+ab2 成立,
只需证(a+b)(a2-ab+b2)>ab(a+b)成立.
又因为a>0,故只需证a2-ab+b2>ab成立,
而依题设a≠b,则(a-b)2>0显然成立,由此命题得证.
法二:(综合法)∵a≠b,∴a-b≠0,
∴a2-2ab+b2>0,∴a2-ab+b2>ab(*).
而a,b均为正数,∴a+b>0,
∴(a+b)(a2-ab+b2)>ab(a+b),
∴a3+b3>a2b+ab2 成立.
点评 本题主要考查用分析法和综合法证明不等式,此题还可用比较法证明,体会不同方法间的区别联系,属于基础题.

练习册系列答案
相关题目
7.一块石材表示的几何体的三视图如图所示,则几何体的体积为( )
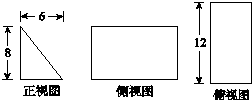

| A. | 96 | B. | 106 | C. | 144 | D. | 288 |
17.下列函数既是奇函数,又在区间[-1,1]上单调递减的是( )
| A. | f(x)=sinx | B. | f(x)=ln$\frac{2-x}{2+x}$ | C. | f(x)=-|x+1| | D. | f(x)=$\frac{1}{2}({e^x}-{e^{-x}})$ |