题目内容
【题目】已知命题p:x∈(-2,1),使等式x2-x-m=0成立,命题q:![]() 表示椭圆.
表示椭圆.
(1)若命题p为真命题,求实数m的取值范围.
(2)判断命题p为真命题是命题q为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个)
【答案】(1){m|![]() ≤m<6}(2)p是q的必要不充分条件
≤m<6}(2)p是q的必要不充分条件
【解析】
(1)把:x∈(-2,1),使等式x2-x-m=0成立转化为方程x2-x-m=0在(-2,1)上有解,即m的取值范围就是函数y=x2-x在(-2,1)上的值域,再求二次函数的值域得答案;
(2)由![]() 表示椭圆求得m的范围,利用集合间的关系结合充分必要条件的判定得答案.
表示椭圆求得m的范围,利用集合间的关系结合充分必要条件的判定得答案.
解:(1)由题意,方程x2-x-m=0在(-2,1)上有解,
即m的取值范围就是函数y=x2-x在(-2,1)上的值域,
函数y=x2-x的对称轴方程为x=![]() ,
,
则当x=![]() 时,有最小值为
时,有最小值为![]() ,
,
当x=-2时,有最大值为6.
可得{m|![]() ≤m<6};
≤m<6};
(2)∵命题q:![]() 表示椭圆为真命题,
表示椭圆为真命题,
∴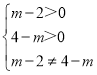 ,解得2<m<3或3<m<4.
,解得2<m<3或3<m<4.
故有{m|![]() ≤m<6}{m|2<m<3或3<m<4}.
≤m<6}{m|2<m<3或3<m<4}.
∴p是q的必要不充分条件.

练习册系列答案
相关题目

