题目内容
(本小题满分16分)
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
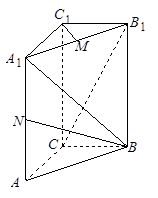
(1)求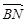 的长;
的长;
(2)求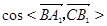 的值;
的值;
(3)求证:A1B⊥C1M(14分).
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
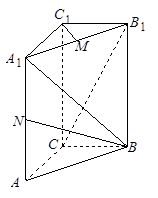
(1)求
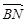 的长;
的长;(2)求
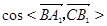 的值;
的值;(3)求证:A1B⊥C1M(14分).
(1) ;
;
(2)见解析。
 ;
; (2)见解析。
本题考查线段的长和两异面直线夹角余弦值的求法,解题时要恰当地建立空间直角坐标系,合理地运用 向量的夹角公式进行求解.以及向量的数量积证明垂直。
(1)以C为原点建立空间直角坐标系,B(0,a,0),N(a,0,a),由此能求出|BN |
(2)A1(a,0,2a),C(0,0,0),B1(0,a,2a),BA1 =(a,-a,2a), CB1=(0,a,2a),再由cos< BA1 , CB1>,能求出BA1,CB1夹角的余弦值.
(3)同理利用垂直来证明数量积为零即可。
(1) ;…..5分
;…..5分
(2)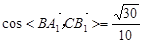 ;…..6分
;…..6分
(3)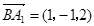 ,
,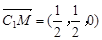 ……5分
……5分
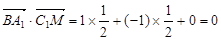
 .
.
(1)以C为原点建立空间直角坐标系,B(0,a,0),N(a,0,a),由此能求出|BN |
(2)A1(a,0,2a),C(0,0,0),B1(0,a,2a),BA1 =(a,-a,2a), CB1=(0,a,2a),再由cos< BA1 , CB1>,能求出BA1,CB1夹角的余弦值.
(3)同理利用垂直来证明数量积为零即可。
(1)
 ;…..5分
;…..5分(2)
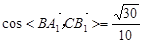 ;…..6分
;…..6分(3)
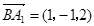 ,
,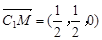 ……5分
……5分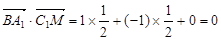
 .
.
练习册系列答案
相关题目
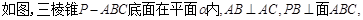
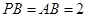 ,
,
 ,P、E在
,P、E在 同侧,连接PE、AE.
同侧,连接PE、AE.
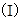 求证:BC//面APE;
求证:BC//面APE;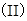 设F是
设F是 ,求直线EF与面APF所成角的大小
,求直线EF与面APF所成角的大小 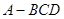 中,面
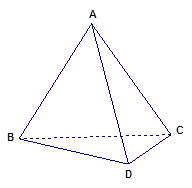
中,面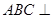 面
面 ,
, 是正三角形,
是正三角形, .
.
 ;
; 所成角的余弦值为
所成角的余弦值为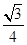 ,求二面角
,求二面角 的大小;
的大小;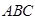
 平面
平面 ,
, 与
与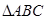 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形,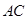 //
//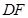 ,四边形
,四边形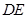 //
//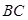 ,
,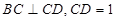 ,点
,点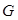 为
为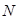 为
为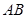 中点,
中点, ,
,
 时,求证:
时,求证: //平面
//平面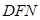
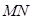 与
与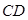 所成角为
所成角为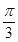 ,试求二面角
,试求二面角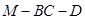 的余弦值.
的余弦值.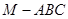 中,
中,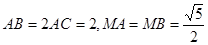 ,
,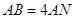 ,
,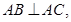 平面
平面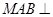 平面
平面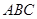 ,
,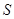 为
为 的中点.
的中点. ;
; 所成角的大小.
所成角的大小.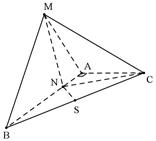
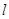 、
、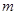 与平面
与平面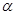 、
、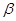 的命题中,正确的是 ( )
的命题中,正确的是 ( )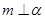 ,
,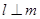 ,则
,则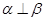 ,
,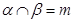 ,
,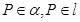 ,且
,且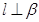
 ,
,
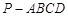 中,
中,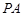
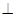 平面
平面 ,底面
,底面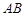 ⊥
⊥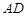 ,
,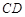 ⊥
⊥ ,
,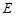 为
为 中点.
中点.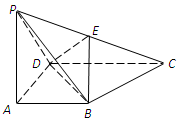
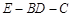 的余弦值.
的余弦值.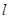 、
、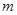 与平面
与平面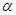 、
、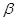 的命题中,正确的是 ( )
的命题中,正确的是 ( )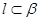 且
且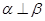 ,则
,则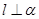 ,
, 且
且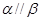 ,则
,则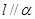 ,
,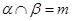 且
且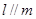 ,则
,则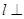 平面
平面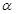 ,直线
,直线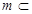 平面
平面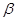 ,则下列四个命题中正确的是 ( )
,则下列四个命题中正确的是 ( )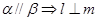 ②
②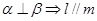 ;③
;③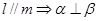 ;④
;④