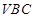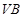题目内容
如图,四棱锥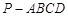 中,
中,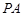
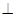 平面
平面 ,底面
,底面 是直角梯形,
是直角梯形,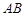 ⊥
⊥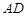 ,
,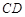 ⊥
⊥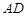 ,
, ,
,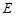 为
为 中点.
中点.
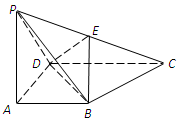
(1) 求证:平面PDC 平面PAD;
平面PAD;
(2) 求证:BE∥平面PAD;
(3)求二面角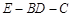 的余弦值.
的余弦值.
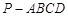 中,
中,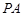
 平面
平面 ,底面
,底面 是直角梯形,
是直角梯形,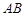 ⊥
⊥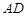 ,
,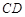 ⊥
⊥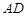 ,
, ,
,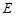 为
为 中点.
中点.
(1) 求证:平面PDC
 平面PAD;
平面PAD;(2) 求证:BE∥平面PAD;
(3)求二面角
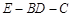 的余弦值.
的余弦值.(1) 证明略(2) 证明略(3)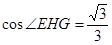
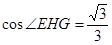
本题主要考查线面垂直的判定定理与面面垂直的判定定理,以及考查线面平行的判定定理,解决此类问题的关键是熟练掌握有关的定理与几何体的结构特征,此题属于基础题,考查学生的空间想象能力与逻辑推理能力.
(1)由题意可得:PA⊥CD,结合CD⊥AD与线面垂直的判定定理可得CD⊥平面PAD,再利用面面垂直的判定定理得到面面垂直.
(2)取PD的中点为F,连接EF,AF,即可得到EF∥CD,CD=2EF,由题中条件可得EF=AB,并且EF∥AB,进而得到四边形ABEF为平行四边形,得到BE∥AF,再利用线面平行的判定定理得到线面平行.
(3)根据面面垂直得到线线垂直,得到两个向量的数量积等于0,求出两个字母之间的关系,设出平面的法向量,根据数量积等于0,做出法向量,进而求出面面角.
解:(I)略--------------(4分)
(II)略
(III)连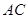 ,取
,取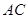 的中点
的中点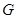 ,连接
,连接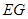 ,则
,则 平面
平面 ,过
,过 作
作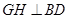 ,
,
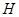 为垂足,连接
为垂足,连接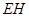 ,可证
,可证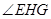 为二面角
为二面角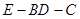 的平面角. -------(10分)
的平面角. -------(10分)
设 ,则可求得
,则可求得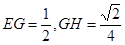 ,
,
从而求得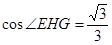 -----------(12分,其他方法比照给分)
-----------(12分,其他方法比照给分)
(1)由题意可得:PA⊥CD,结合CD⊥AD与线面垂直的判定定理可得CD⊥平面PAD,再利用面面垂直的判定定理得到面面垂直.
(2)取PD的中点为F,连接EF,AF,即可得到EF∥CD,CD=2EF,由题中条件可得EF=AB,并且EF∥AB,进而得到四边形ABEF为平行四边形,得到BE∥AF,再利用线面平行的判定定理得到线面平行.
(3)根据面面垂直得到线线垂直,得到两个向量的数量积等于0,求出两个字母之间的关系,设出平面的法向量,根据数量积等于0,做出法向量,进而求出面面角.
解:(I)略--------------(4分)
(II)略
(III)连
 ,取
,取 的中点
的中点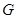 ,连接
,连接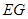 ,则
,则 平面
平面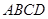 ,过
,过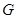 作
作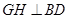 ,
,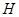 为垂足,连接
为垂足,连接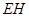 ,可证
,可证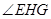 为二面角
为二面角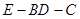 的平面角. -------(10分)
的平面角. -------(10分)设
 ,则可求得
,则可求得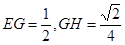 ,
,从而求得
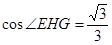 -----------(12分,其他方法比照给分)
-----------(12分,其他方法比照给分)
练习册系列答案
相关题目
 中,所有的棱长都为2,
中,所有的棱长都为2,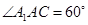 .
.
 ;
; 与平面
与平面 所成的锐角的余弦值.
所成的锐角的余弦值.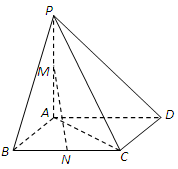
 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
,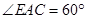 ,
,
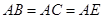 .
.  上是否存在一点
上是否存在一点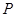 ,使得
,使得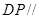 平面
平面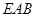 ?请证明你的结论;
?请证明你的结论; 与平面
与平面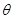 的余弦值。
的余弦值。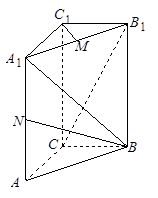
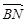 的长;
的长;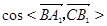 的值;
的值;
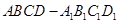 的棱
的棱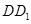 的中点,给出命题
的中点,给出命题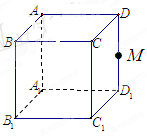
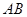 、
、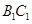 都相交;
都相交;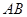 是
是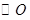 的直径,点
的直径,点 是
是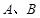 重合),过动点
重合),过动点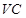 垂直于
垂直于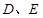 分别是
分别是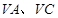 的中点,则下列结论错误的是
的中点,则下列结论错误的是 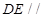 平面
平面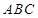
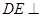 平面
平面