题目内容
5.设函数f(x)=ex-x-2(1)求函数f(x)在x=1处的切线方程;
(2)若k为整数,且当x>0时,(x-k)f′(x)+x+1>0恒成立,求k的最大值.
分析 (1)求出原函数的导函数,得到函数在x=1时的导数,然后由直线方程的点斜式求得切线方程;
(2)把当x>0时,(x-k)f′(x)+x+1>0恒成立,转化为k<$\frac{x+1}{{e}^{x}-1}$+x,构造函数g(x)=$\frac{x+1}{{e}^{x}-1}$+x,利用导数求得函数g(x)的最小值的范围得答案.
解答 解:(1)函数f(x)=ex-x-2的导数为:
f′(x)=ex-1,
函数f(x)在x=1处的切线斜率为k=e-1,
切点为(1,e-3),
即有函数f(x)在x=1处的切线方程为y-(e-3)=(e-1)(x-1),
即为y=(e-1)x-2;
(2)当x>0时,ex-1>0,
∴不等式,(x-k)f′(x)+x+1>0可以变形如下:
(x-k)(ex-1)+x+1>0,即k<$\frac{x+1}{{e}^{x}-1}$+x①
令g(x)=$\frac{x+1}{{e}^{x}-1}$+x,则g′(x)=$\frac{{e}^{x}({e}^{x}-x-2)}{({e}^{x}-1)^{2}}$,
函数h(x)=ex-x-2在(0,+∞)上单调递增,而h(1)<0,h(2)>0,
∴h(x)在(0,+∞)上存在唯一的零点,
故g′(x)在(0,+∞)上存在唯一的零点.
设此零点为a,则a∈(1,2).
当x∈(0,a)时,g′(x)<0;当x∈(a,+∞)时,g′(x)>0;
∴g(x)在(0,+∞)上的最小值为g(a).由g′(a)=0,可得ea=a+2,
∴g(a)=a+1∈(2,3),
由于①式等价于k<g(a).
故整数k的最大值为2.
点评 本题考查了利用导数求过曲线上某点处的切线方程,考查了函数恒成立问题,着重考查了数学转化思想方法,考查了函数最值的求法,属中档题.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案| A. | 6 | B. | 10 | C. | 12 | D. | 20 |
| A. | 2$\sqrt{3}$ | B. | $\sqrt{15}$ | C. | 4 | D. | $\sqrt{13}$ |
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{7}$ |
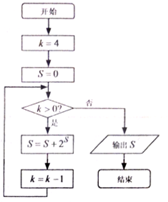
| A. | 2059 | B. | 1035 | C. | 11 | D. | 3 |