题目内容
19.同时掷两个骰子,向上的点数不相同的概率为( )| A. | $\frac{5}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
分析 列举出所有情况,及出现相同点数的情况数,先求出向上点数相同的概率,进而利用对立事件概率减法公式,得到答案.
解答 解:同时掷两个骰子,向上的点数共有36种不同情况,分别为:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
故向上的点数相同的概率P=$\frac{6}{36}$=$\frac{1}{6}$,
故向上的点数不相同的概率P=1-$\frac{1}{6}$=$\frac{5}{6}$,
故选:A
点评 如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
5.给出如下“三段论”推理:
因为整数是自然数,…大前提
而-5是整数,…小前提
所以-5是自然数.…结 论
则( )
因为整数是自然数,…大前提
而-5是整数,…小前提
所以-5是自然数.…结 论
则( )
| A. | 这个推理的形式错误 | B. | 这个推理的大前提错误 | ||
| C. | 这个推理的小前提错误 | D. | 这个推理正确 |
6.某四面体的三视图如图所示,该四面体四个面的面积中最大的是( )
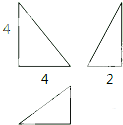

| A. | 8 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{5}$ | D. | 10 |
7.设a=log0.32,b=log32,c=20.3,则a,b,c的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<a<c |
11.角α终边上有一点(-a,2a)(a<0),则sinα=( )
| A. | -$\frac{2\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |