题目内容
4．一个几何体的三视图如图所示，则该几何体的体积为$\frac{13}{2}$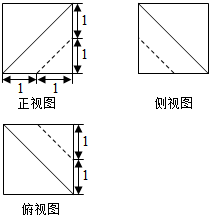
分析 根据几何体的三视图，得出该几何体是正方体在相对的两个顶点处各去掉一个三棱锥，结合图中数据，即可求出它的体积．
解答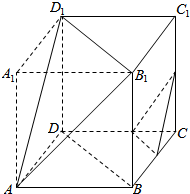 
解：根据几何体的三视图，得，
该几何体是棱长为2的正方体，在相对的两个顶点处各去掉一个三棱锥，
如图所示；
所以，该几何体的体积为
V=23-$\frac{1}{3}$×$\frac{1}{2}$×22×2-$\frac{1}{3}$×12×1
=8-$\frac{4}{3}$-$\frac{1}{6}$
=$\frac{13}{2}$．
点评 本题考查了利用几何体的三视图求体积的应用问题，是基础题目．
练习册系列答案
相关题目
12．$\frac{（sin\frac{π}{10}+cos\frac{π}{10}）（sin\frac{3π}{20}+cos\frac{3π}{20}）}{cos\frac{π}{10}cos\frac{3π}{20}}$的值等于（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | 1+$\sqrt{2}$ | D． | 2+$\sqrt{2}$ |