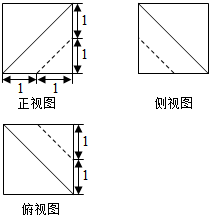
题目内容
16.已知向量$\overrightarrow{a}$=($\sqrt{2}$,3),$\overrightarrow{b}$=(-1,2),若m$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$平行,则m=$-\frac{1}{2}$.分析 由已知向量的坐结合向量的数乘及坐标加减法运算求得m$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$的坐标,再由m$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$平行列式求得答案.
解答 解:∵$\overrightarrow{a}$=($\sqrt{2}$,3),$\overrightarrow{b}$=(-1,2),
∴m$\overrightarrow{a}$+$\overrightarrow{b}$=$m(\sqrt{2},3)+(-1,2)=(\sqrt{2}m-1,3m+2)$,
$\overrightarrow{a}$-2$\overrightarrow{b}$=$(\sqrt{2},3)-2(-1,2)=(2+\sqrt{2},-1)$.
由m$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$平行,
得$(\sqrt{2}m-1)×(-1)-(3m+2)×(2+\sqrt{2})=0$,解得:m=$-\frac{1}{2}$.
故答案为:$-\frac{1}{2}$.
点评 共线问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若$\overrightarrow{a}$=(a1,a2),
$\overrightarrow{b}$=(b1,b2),则$\overrightarrow{a}$⊥$\overrightarrow{b}$?a1a2+b1b2=0,$\overrightarrow{a}$∥$\overrightarrow{b}$?a1b2-a2b1=0,是基础题.

 初中暑期衔接系列答案
初中暑期衔接系列答案| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 74 | 76 | 72 | 70 | 78 |
| A. | 80 | B. | 90 | C. | 86 | D. | 70 |