题目内容

5．如图所示，ABCD-A1B1C1D1是正方体，在图①中，E，F分别是D1C1，B1B的中点，画出图①②中有阴影的平面与平面ABCD的交线，并给出证明．

分析 （1）根据正方体的几何特征，我们取CD的中点P，连接PB并延长交EF的延长线于Q．连接AQ，即可得到满足条件的交线；
（2）根据线面平行的性质定理，过B点作A1C1的平行线MN，即可得到满足条件的交线；

解答 解：如图所示：取CD的中点P，连接PB并延长交EF的延长线于Q．连接AQ，过B点作A1C1的平行线MN即可得到满足条件的交线AQ和MN；

理由如下：∵E，F分别是D1C1，B1B的中点，P是BC的中点，
则EP∥B1B，EP=B1B，
则EFBP共面，故EF与PB相交于Q点，
则Q∈直线EF，进而Q∈平面AEF，
Q∈PB，进而Q∈平面ABCD，
故Q是平面AEF与平面ABCD的公共点，
又由A也是平面AEF与平面ABCD的公共点，
故直线AQ即为两个平面的交线；
由正方体的两个底面平行，A1C1?平面A1B1C1D1，
故A1C1∥平面ABCD，
则过A1C1的平面A1C1B与平面ABCD的交线与A1C1平行，
而经过直线外一点有且只有一条直线与已知直线平行，
故过B点作A1C1的平行线MN即为两个平面的交线．

点评 本题考查的知识点是正方体的几何特征，空间直线与平面的位置关系，难度中档．

练习册系列答案
相关题目
15．已知集合A={x|3≤x＜7}，B={x|2＜x＜10}，求∁R（A∩B），A∪（∁RB）
16．已知函数y=ax+b（a＞1，b＞0）的图象经过点P（1，3），则$\frac{4}{a-1}$+$\frac{1}{b}$的最小值为$\frac{9}{2}$．
13．若A，B为椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴两端点，Q为椭圆上一点，使∠AQB=120°，求此椭圆离心率最小值为$\frac{\sqrt{6}}{3}$．
20．已知函数f（x）=asin2x一$\frac{1}{3}$sin3x（a为常数）在x=$\frac{π}{3}$处取得极值，则a的值为2．
10．椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$（a＞b），过右焦点F且斜率为2$\sqrt{6}$的直线与椭圆及y轴交于B，M点，B分$\overrightarrow{MF}$所成的比为2，求椭圆的离心率．
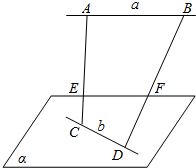17．如图所示，a，b是异面直线，A，B∈a，C，D∈b，E，F分别为线段AC，BD的中点，判断直线EF和a的位置关系，并证明你的结论．
14．在风平浪静的海面上，有一战斗机要去执行一项紧急飞行任务，而航空母舰的弹射系统出了故障，无法在短时间内修复．已知飞机在跑道上加速时，可能产生的最大加速度为5m/s2，起飞速度为50m/s．跑道长为100m．经过计算发现在这些条件下飞机根本无法安全起飞（请你计算，作出判断）．航空母舰不得不在海面上沿起飞方向运动，从而使飞机获得初速度，达到安全起飞的目的，那么航空母舰行驶的速度至少为多大？
15．将下列符号表示转换成文字描述：
（1）$\left.\begin{array}{l}{A∈α}\\{B∈α}\end{array}\right\}$⇒直线AB?α；
（2）$\left.\begin{array}{l}{P∈α}\\{P∈β}\end{array}\right\}$⇒α∩β=l，且P∈l．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网