题目内容
若直线 (
( )被圆
)被圆 截得的弦长为4,则
截得的弦长为4,则 的最小值为( )
的最小值为( )
A. | B. | C.2 | D.4 |
D
解析试题分析:易知圆心为(-1,2),圆的半径为2,因为直线被圆截得的弦长为4,所以直线过圆心,所以-2a-2b+2=0,即a+b=1。又 ,
,
所以 。
。
考点:直线与圆的位置关系;基本不等式;点到直线的距离公式。
点评:做本题的关键是灵活应用“1”代换,使 变形为
变形为 ,从而就达到积为定值的目的,应用基本不等式。“1”代换是我们常用的方法,我们要注意熟练掌握。
,从而就达到积为定值的目的,应用基本不等式。“1”代换是我们常用的方法,我们要注意熟练掌握。

练习册系列答案
相关题目
圆 和圆
和圆 的位置关系为( )
的位置关系为( )
| A.相交 | B.内切 | C.外切 | D.外离 |
已知 ,则函数
,则函数 的零点个数为
的零点个数为
| A.1 | B.2 | C.3 | D.4 |
两圆相交于点 ,两圆的圆心均在直线
,两圆的圆心均在直线 上,则
上,则 的值为( )
的值为( )
A. | B. | C. | D. |
若 ,则直线
,则直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B.1 | C. | D. |
直线 与圆
与圆 的位置关系是 ( )
的位置关系是 ( )
| A.相切 | B.相交但直线不过圆心 | C.直线过圆心 | D.相离 |
 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、 ,则称P优于
,则称P优于 ,如果
,如果
 与圆
与圆 的两个交点,则
的两个交点,则 ( )
( ) D.
D.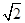
 绕着其与
绕着其与 轴的交点逆时针旋转
轴的交点逆时针旋转 得到直线m,则m与圆
得到直线m,则m与圆 截得弦长为( )
截得弦长为( )


