题目内容
直线 与圆
与圆 的位置关系是 ( )
的位置关系是 ( )
| A.相切 | B.相交但直线不过圆心 | C.直线过圆心 | D.相离 |
B
解析试题分析:考查直线与圆的位置关系,可知运用代数的方法联立方程组,得到的一元二次方程中判别式的情况来确定结论,当 ,说明相交,当
,说明相交,当 ,说明相离,当
,说明相离,当 ,说明是相切。或者常用圆心到直线的距离与圆的半径的关系来判定。由于圆
,说明是相切。或者常用圆心到直线的距离与圆的半径的关系来判定。由于圆 的圆心坐标为(0,0),半径为1,则圆心到直线
的圆心坐标为(0,0),半径为1,则圆心到直线 的距离
的距离 ,那么可知直线与圆相交,并且(0,0)点不在直线y=x+1上,因此是相交且不过圆心,故选B.
,那么可知直线与圆相交,并且(0,0)点不在直线y=x+1上,因此是相交且不过圆心,故选B.
考点:本试题主要是考查了直线与圆的位置关系的运用。
点评:解决该试题常用的方法就是运用点到直线的距离公式,结合圆的半径r的大小和d的关系来得到,d=r,相切,0<d<r,相交,d>r,相离。

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
若直线 (
( )被圆
)被圆 截得的弦长为4,则
截得的弦长为4,则 的最小值为( )
的最小值为( )
A. | B. | C.2 | D.4 |
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
| A.1 | B. | C.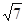 | D.3 |
若直线 与曲线
与曲线 有公共点,则
有公共点,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
过圆 上一点
上一点 的切线方程是( )
的切线方程是( )
A. | B. | C. | D. |
已知圆 与直线
与直线 及
及 都相切,圆心在直线
都相切,圆心在直线 上,则圆
上,则圆 的方程为( )
的方程为( )
A. | B. |
C. | D. |
若 ,则直线
,则直线 被圆
被圆 所截得的弦长为
所截得的弦长为
A. | B.1 | C. | D. |
若直线 过圆
过圆 的圆心,则
的圆心,则 的值为 ( )
的值为 ( )
A. 1 1 | B.1 | C.3 | D. 3 3 |
 与圆
与圆 有公共点
有公共点 则斜率
则斜率 的取值范围是( )
的取值范围是( )






