题目内容
【题目】已知数列![]() 满足
满足 ![]() .
.
(1)证明:当![]() 时,
时,![]() ;
;
(2)证明:![]() (
(![]() );
);
(3)证明:![]() 为自然常数.
为自然常数.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)用数学归纳法证明,先证![]() 成立,再假设当
成立,再假设当![]() 时结论成立,即
时结论成立,即![]() ,再证当
,再证当![]() ,
,![]() 成立,这一步需要用到
成立,这一步需要用到![]() 这一假设
这一假设
(2)先观察证明的恒等式,发觉右侧出现了裂项的基本形式,故可考虑将式子作如下变形处理![]() ,通过移项可得
,通过移项可得![]() ,再采用叠加法即可求得
,再采用叠加法即可求得
由递推公式和(1)的结论有![]()
变形得![]() ,两边同取对数得
,两边同取对数得![]() ,再利用导数公式
,再利用导数公式![]() ,可得
,可得![]()
即![]() ,再采用累加法通过变形最后即可得到
,再采用累加法通过变形最后即可得到![]()
(1)(用数学归纳法证明)
①当![]() 时,
时,![]() ,
,
所以结论成立;
②假设当![]() 时结论成立,即
时结论成立,即![]() .
.
则当![]() 时
时
![]()
所以![]() 时,结论成立.
时,结论成立.
由①②可知,当![]() 时,
时,![]() 成立
成立
(2)由题意得![]()
所以![]()
所以![]() ,
,
![]() ,
,
![]() ,
,
……
![]() ,
,
以上各式两边分别相加可得![]() ,
,
又![]() ,所以
,所以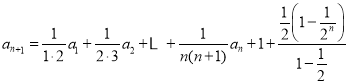
![]() .
.
(3)由题意得![]() ,
,
∴![]() ,
,
∴![]() ,(利用了导数公式
,(利用了导数公式![]() 的性质)
的性质)
∴![]() ,
,
由累加法得
![]()
![]() ,
,
所以![]() ,
,
所以![]() ,
,
故![]() ,
,
所以![]() 为自然常数.
为自然常数.

【题目】某市调硏机构对该市工薪阶层对“楼市限购令”态度进行调查,抽调了50名市民,他们月收入频数分布表和对“楼市限购令”赞成人数如下表:
月收入(单位:百元) |
|
|
|
|
|
|
频数 | 5 |
| 10 | 5 | 5 | |
频率 | 0.1 |
|
| 0.2 | 0.1 | 0.1 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
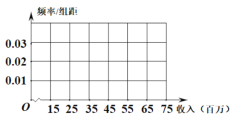
(1)若所抽调的50名市民中,收入在![]() 的有15名,求
的有15名,求![]() ,
,![]() ,
,![]() 的值,并完成频率分布直方图.
的值,并完成频率分布直方图.
(2)若从收入(单位:百元)在![]() 的被调查者中随机选取2人进行追踪调查,选中的2人中恰有
的被调查者中随机选取2人进行追踪调查,选中的2人中恰有![]() 人赞成“楼市限购令”,求
人赞成“楼市限购令”,求![]() 的分布列与数学期望.
的分布列与数学期望.
(3)从月收入频率分布表的6组市民中分别随机抽取3名市民,恰有一组的3名市民都不赞成“楼市限购令”,根据表格数据,判断这3名市民来自哪组的可能性最大?请直接写出你的判断结果.
【题目】某市环保部门为了让全市居民认识到冬天烧煤取暖对空气![]() 数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数
数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数![]() 与空气
与空气![]() 数值不合格的天数
数值不合格的天数![]() 进行统计分析,得出下表数据:
进行统计分析,得出下表数据:
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
(1)以统计数据为依据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)求出的线性回归方程,预测该市烧煤取暖的天数为20时空气![]() 数值不合格的天数.
数值不合格的天数.
参考公式: ,
,![]() .
.