题目内容
10.已知p:关于x的方程x2+mx+1=0有两个不相等的负实根;q:关于x的不等式4x2+4(m-2)x+1>0的解集为R.若p∨q为真,p∧q为假,求实数m的取值范围.分析 若命题p为真命题,可得$\left\{\begin{array}{l}{△={m}^{2}-4>0}\\{-m<0}\end{array}\right.$,解得m.若命题q为真命题,可得△<0,解得m.若p或q为真命题、p且q为假命题,可得p与q必然一真一假,解出即可.
解答 解:命题p:方程x2+mx+1=0有两个不相等的负实根,∴$\left\{\begin{array}{l}{△={m}^{2}-4>0}\\{-m<0}\end{array}\right.$,解得m>2.
命题q:不等式4x2+4(m-2)x+1>0的解集为R,∴△=16(m-2)2-16<0,解得1<m<3.
p∨q为真命题、p∧q为假命题,
∴p,q一真一假;
①若p真且q假,则$\left\{\begin{array}{l}{m>2}\\{m≤1或m≥3}\end{array}\right.$,解得m≥3;
②若p假且q真,则$\left\{\begin{array}{l}{m≤2}\\{1<m<3}\end{array}\right.$,解得1<m≤2;
综上可知实数m的取值范围是(1,2]∪[3,+∞).
点评 本题考查了一元二次不等式的解集与判别式的关系、简易逻辑的判定,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
20.已知函数y=$\frac{\sqrt{1-x}}{2{x}^{2}-3x-2}$的定义域为( )
| A. | (-∞,1] | B. | (-∞,2] | C. | (-∞,-$\frac{1}{2}$)∩(-$\frac{1}{2}$,1] | D. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1] |
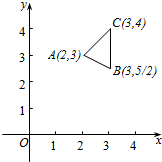 已知点(x,y)在△ABC所包围的阴影区域内(包含边界),若B是使得z=ax-y取得最大值的最优解,则实数a的取值范围为[-$\frac{1}{2}$,+∞).
已知点(x,y)在△ABC所包围的阴影区域内(包含边界),若B是使得z=ax-y取得最大值的最优解,则实数a的取值范围为[-$\frac{1}{2}$,+∞). 如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点.
如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点.