题目内容
3.已知数列{an}的前n项和为Sn,且满足an+2SnSn-1=0(n≥2,n∈N),a1=$\frac{1}{2}$.(1)求证:数列{$\frac{1}{S_n}$}为等差数列.并求数列{an}的通项公式an.
(2)记数列{bn}的通项公式为bn=$\frac{1}{{{2^n}{S_n}}}$,Tn=b1+b2+…+bn,求Tn的值.
分析 (1)当n≥2时,化简Sn-Sn-1+2SnSn-1=0,从而可得$\frac{1}{S_n}-\frac{1}{{{S_{n-1}}}}$=2及$\frac{1}{S_1}=\frac{1}{a_1}$=2;从而证明{$\frac{1}{S_n}$}是等差数列;再求数列{an}的通项公式an;
(2)化简bn=$\frac{1}{{{2^n}{S_n}}}$=$\frac{n}{{{2^{n-1}}}}$;从而可得Tn=b1+b2+…+bn=1+$\frac{2}{2}$+$\frac{3}{2^2}$+…+$\frac{n-1}{{{2^{n-2}}}}$+$\frac{n}{{{2^{n-1}}}}$,2Tn=2+$\frac{2}{2^0}$+$\frac{3}{2}$+…+$\frac{n-1}{{{2^{n-3}}}}$+$\frac{n}{{{2^{n-2}}}}$;利用错位相减法求Tn的值.
解答 解:(1)当n≥2时,an=Sn-Sn-1,又an+2SnSn-1=0,
则有Sn-Sn-1+2SnSn-1=0①,
若Sn=0,则a1=S1=0与a1=$\frac{1}{2}$矛盾,故Sn≠0;
由①得$\frac{1}{S_n}-\frac{1}{{{S_{n-1}}}}$=2,又$\frac{1}{S_1}=\frac{1}{a_1}$=2;
所以数列{$\frac{1}{S_n}$}是以2为首项,公差为2的等差数列.
故$\frac{1}{S_n}$=2+2(n-2)=2n,Sn=$\frac{1}{2n}$;
当n≥2时,an=-2SnSn-1=-$\frac{1}{2n(n-1)}$,而n=1时,a1=$\frac{1}{2}$;
故${a_n}=\left\{\begin{array}{l}\frac{1}{2},n=1\\-\frac{1}{2n(n-1)},n≥2\end{array}\right.$;
(2)bn=$\frac{1}{{{2^n}{S_n}}}$=$\frac{n}{{{2^{n-1}}}}$;
∵Tn=b1+b2+…+bn=1+$\frac{2}{2}$+$\frac{3}{2^2}$+…+$\frac{n-1}{{{2^{n-2}}}}$+$\frac{n}{{{2^{n-1}}}}$①,
2Tn=2+$\frac{2}{2^0}$+$\frac{3}{2}$+…+$\frac{n-1}{{{2^{n-3}}}}$+$\frac{n}{{{2^{n-2}}}}$②;
∴②-①得,Tn=3+$\frac{1}{2}$+$\frac{1}{2^2}$+…+$\frac{1}{{{2^{n-2}}}}$-$\frac{n}{{{2^{n-1}}}}$=4-$\frac{n+2}{{{2^{n-1}}}}$;
故Tn=4-$\frac{n+2}{{{2^{n-1}}}}$.
点评 本题考查了等差数列的判断与证明及数列前n项和的应用,同时考查了错位相减法的应用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 最大值为6 | B. | 最小值为6 | C. | 最大值为36 | D. | 最小值为36 |
| A. | (x+1)2+(y+1)2=2 | B. | (x+1)2+(y-1)2=2 | C. | (x+1)2+(y+1)2=4 | D. | (x+1)2+(y-1)2=4 |
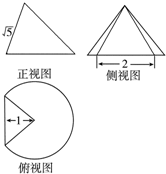 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )| A. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$+1 | B. | 2$\sqrt{5}$+3$\sqrt{3}$π+$\frac{3π}{2}$+1 | C. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$ | D. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{π}{2}$+1 |
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | -1 | D. | $\frac{{\sqrt{3}-1}}{2}$ |
| A. | 3+$\sqrt{3}$ | B. | 3-$\sqrt{3}$ | C. | 3+$\sqrt{7}$ | D. | 3-$\sqrt{7}$ |