题目内容
17.已知数列{an}满足a1=1,an=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1(n>1),则数列{an}的通项公式an=n,若an=2013,则n=2013.分析 通过an=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1与an+1=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1+$\frac{1}{n}$an作差、整理可知$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,利用累乘法计算即得结论.
解答 解:∵an=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1(n>1),
∴an+1=a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1+$\frac{1}{n}$an,
两式相减得:an+1-an=$\frac{1}{n}$an,即an+1=$\frac{n+1}{n}$an,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,
$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n}{n-1}$,
$\frac{{a}_{n-1}}{{a}_{n-2}}$=$\frac{n-1}{n-2}$,
…
$\frac{{a}_{2}}{{a}_{1}}$=$\frac{2}{1}$,
累乘得:$\frac{{a}_{n}}{{a}_{1}}$=$\frac{n}{1}$,
∴an=na1=n,
故答案为:n,2013.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
7.从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下: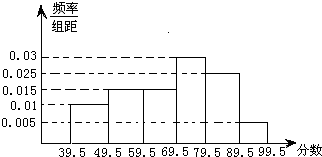
估计这次环保知识竞赛的及格率(60分及以上为及格)是( )

估计这次环保知识竞赛的及格率(60分及以上为及格)是( )
| A. | 7.5% | B. | 70% | C. | 2.5% | D. | 75% |
8.甲、乙两人从4门课程中各选修1门,则不同的选法有( )
| A. | 8种 | B. | 12种 | C. | 16种 | D. | 24种 |
12.$\frac{(sin\frac{π}{10}+cos\frac{π}{10})(sin\frac{3π}{20}+cos\frac{3π}{20})}{cos\frac{π}{10}cos\frac{3π}{20}}$的值等于( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |