题目内容

16．5名学生和2名老师排成一排照相，2名老师不在两边且不相邻的概率为$\frac{2}{7}$．

分析 由排列组合的知识可得总的排法和2名老师不在两边且不相邻的排法，由概率公式可得．

解答 解：7人排队共有${A}_{7}^{7}$种方法，
其中2名老师不在两边且不相邻，
可先排5名学生共${A}_{5}^{5}$种方法，再从产生的中间4个空位任选2个排列2位老师
共${A}_{4}^{2}$种方法，由分步计数原理可得共${A}_{5}^{5}•{A}_{4}^{2}$种方法，
故所求概率P=$\frac{{A}_{5}^{5}•{A}_{4}^{2}}{{A}_{7}^{7}}$=$\frac{2}{7}$．
故答案为：$\frac{2}{7}$．

点评 本题考查排列组合在古典概型中的应用，属基础题．

练习册系列答案
相关题目
18．判断集合A是否为集合B的子集，若是打“√”，若不是打“×”．
（1）A={1，3，5}，B={1，2，3，4，5，6}．√；
（2）A={1，3，5}，B={1，3，6，9}．×；
（3）A={0}，B={x|x2+1=0}．×；
（4）A={a，b，c，d}，B={d，b，c，a}．√．
7．从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布直方图如下：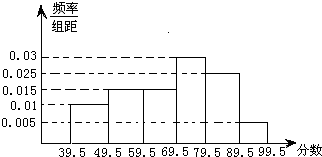
估计这次环保知识竞赛的及格率（60分及以上为及格）是（　　）
A．7.5%B．70%C．2.5%D．75%
4．给出算法
第一步，输入n=5．
第二步，令i=1，S=1．
第三步，判断i≤n是否成立，若不成立，输出S，结束算法，若成立，执行下一步．
第四步，令S的值乘以i，仍用S表示，令i的值增加1，仍用i表示，返回第三步．
该算法的功能是计算并输出S=1×2×3×4×5的值．
11．如图，已知A，B，C是直线m上的三点，且|AB|=|BC|=6，⊙O切直线m于点A，又过B，C作异于直线m的两切线，切点分别为D，E，设两切线交于点P．

（1）求点P的轨迹E的方程；
（2）证明：已知S是轨迹E上异于A1，A2（轨迹E顶点）的一点，直线A1S，A2S分别交直线l：x=t（t为常数）于不同两点M，N，点Q在直线l上，若Q为线段MN的中点，则直线SQ与轨迹E有且只有一个公共点S．
1．已知数列{an}与{bn}满足下列关系：a1=2a，an+1=$\frac{1}{2}$（an+$\frac{{a}^{2}}{{a}_{n}}$），bn=$\frac{{a}_{n}+a}{{a}_{n}-a}$（n∈N*），其中a＞0．
（1）求数列{bn}的通项公式，并证明：$\frac{{a}_{n}-a}{{a}_{n+1}-a}$=${3}^{{2}^{n-1}}$+1；
（2）设Sn是数列{an}的前n项和，当n≥2时，与（n+$\frac{4}{3}$）a是否有确定的大小关系？若有，请加以证明；若没有，请说明理由．
8．甲、乙两人从4门课程中各选修1门，则不同的选法有（　　）
A．8种B．12种C．16种D．24种
5．已知数列{an}的前n项和为Sn，且Sn=n-5an-85，n∈N*．
（1）证明：{an-1}是等比数列；
（2）求数列{an}的通项公式．
6．已知a是实数，如果任意实数x都是不等式|x+1|+|x|-|x+a|＞0的解，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网