题目内容
【题目】如图,在以A,B,C,D,E,F为顶点的多面体中,AF⊥平面ABCD,DE⊥平面ABCD,AD∥BC,AB=CD,∠ABC=60°,BC=AF=2AD=4DE=4. 
(Ⅰ)请在图中作出平面α,使得DEα,且BF∥α,并说明理由;
(Ⅱ)求直线EF与平面BCE所成角的正弦值.
【答案】解:(Ⅰ)取BC的中点G,连接EG,DG,则平面EDG为所求. ∵AD=2,BG=2,AD∥BC,
∴四边形ADGB是平行四边形,
∴AB∥DG,
∵AB平面EDG,DG平面EDG,
∴AB∥平面EDG.
同理AF∥平面EDG,
∵AB∩AF=A,
∴平面ABF∥平面EDG,
∵FB平面ABF,
∴BF∥平面EDG;
(Ⅱ)以点A为坐标原点,AD为y轴,AF为z轴,过A垂直于AD的直线为x轴,建立如图所示的坐标系,则F(0,0,4),E(0,2,1),B( ![]() ,﹣1,0),C(
,﹣1,0),C( ![]() ,3,0),
,3,0),
∴ ![]() =(0,﹣2,3),
=(0,﹣2,3), ![]() =(0,4,0),
=(0,4,0), ![]() =(﹣
=(﹣ ![]() ,3,1),
,3,1),
设平面BCE的法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,
,
取 ![]() =(
=( ![]() ,0,3),则直线EF与平面BCE所成角的正弦值=
,0,3),则直线EF与平面BCE所成角的正弦值= ![]() =
= ![]() .
.
【解析】(Ⅰ)取BC的中点G,连接EG,DG,证明平面ABF∥平面EDG,可得结论;(Ⅱ)建立如图所示的坐标系,求出平面BCE的法向量,利用向量方法求直线EF与平面BCE所成角的正弦值.
【考点精析】本题主要考查了直线与平面平行的判定和空间角的异面直线所成的角的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则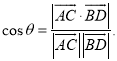 才能正确解答此题.
才能正确解答此题.

【题目】某投资公司现提供两种一年期投资理财方案,一年后投资盈亏的情况如表:
投资股市 | 获利40% | 不赔不赚 | 亏损20% | 购买基金 | 获利20% | 不赔不赚 | 亏损10% |
概率P | | | | 概率P | p | | q |
(I)甲、乙两人在投资顾问的建议下分别选择“投资股市”和“购买基金”,若一年后他们中至少有一人盈利的概率大于 ![]() ,求p的取值范围;
,求p的取值范围;
(II)某人现有10万元资金,决定在“投资股市”和“购买基金”这两种方案中选出一种,若购买基金现阶段分析出 ![]() ,那么选择何种方案可使得一年后的投资收益的数学期望值较大?
,那么选择何种方案可使得一年后的投资收益的数学期望值较大?
