题目内容

【题目】已知函数f（x）= ，g（x）=af（x）﹣|x﹣1|．
（Ⅰ）当a=0时，若g（x）≤|x﹣2|+b对任意x∈（0，+∞）恒成立，求实数b的取值范围；
（Ⅱ）当a=1时，求g（x）的最大值．

【答案】解：（Ⅰ）当a=0时，g（x）=﹣|x﹣1|，∴﹣|x﹣1|≤|x﹣2|+b， ∴﹣b≤|x﹣1|+|x﹣2|，
∵|x﹣1|+|x﹣2|≥|x﹣1+2﹣x|=1，∴﹣b≤1，∴b≥﹣1
（Ⅱ）当a=1时，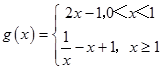
可知g（x）在（0，1）上单调递增，在（1，+∞）单调递减
∴g（x）max=g（1）=1
【解析】．…（10分）
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识，掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值．

练习册系列答案
相关题目

【题目】已知函数f（x）=x3+ax2+bx+c有两个极值点x1 ， x2 ， 若x2＜f（x1）＜x1 ， 则关于x的方程3（f（x））2+2af（x）+b=0的不同实根个数可能为（ ）
A.3，4，5
B.4，5，6
C.2，4，5
D.2，3，4

【题目】设f（x）是定义在R上的恒不为零的函数，对任意实数x，y∈R，都有f（x）f（y）=f（x+y），若a1= ，an=f（n）（n∈N*），则数列{an}的前n项和Sn的取值范围是（ ）
A.[ ，2）
B.[ ，2]
C.[ ，1）
D.[ ，1]

【题目】已知m、n是两条不同的直线，α、β是两个不同的平面，给出下列命题： ①若α⊥β，m∥α，则m⊥β；
②若m⊥α，n⊥β，且m⊥n，则α⊥β；
③若m⊥β，m∥α，则α⊥β；
④若m∥α，n∥β，且m∥n，则α∥β．
其中正确命题的序号是（ ）
A.①④
B.②③
C.②④
D.①③

【题目】如图，在以A，B，C，D，E，F为顶点的多面体中，AF⊥平面ABCD，DE⊥平面ABCD，AD∥BC，AB=CD，∠ABC=60°，BC=AF=2AD=4DE=4．
（Ⅰ）请在图中作出平面α，使得DEα，且BF∥α，并说明理由；
（Ⅱ）求直线EF与平面BCE所成角的正弦值．

【题目】如图，在多面体ABCDM中，△BCD是等边三角形，△CMD是等腰直角三角形，∠CMD=90°，平面CMD⊥平面BCD，AB⊥平面BCD．
（Ⅰ）求证：CD⊥AM；
（Ⅱ）若AM=BC=2，求直线AM与平面BDM所成角的正弦值．

【题目】已知函数（其中为常数）.

（1）判断函数的奇偶性；

（2）若不等式在时有解，求实数的取值范围；

（3）设，是否存在正数，使得对于区间上的任意三个实数，，，都存在以，，为边长的三角形？若存在，试求出这样的的取值范围；若不存在，请说明理由.

【题目】将函数 图象上所有点的横坐标缩短为原来的 ，纵坐标不变，再向右平移 个单位长度，得到函数y=g（x）的图象，则下列说法正确的是（ ）
A.函数g（x）的一条对称轴是
B.函数g（x）的一个对称中心是
C.函数g（x）的一条对称轴是
D.函数g（x）的一个对称中心是

【题目】已知函数f（x）=9x﹣2a3x+3：
（1）若a=1，x∈[0，1]时，求f（x）的值域；
（2）当x∈[﹣1，1]时，求f（x）的最小值h（a）；
（3）是否存在实数m、n，同时满足下列条件：①n＞m＞3；②当h（a）的定义域为[m，n]时，其值域为[m2 ， n2]，若存在，求出m、n的值，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网