题目内容
【题目】正方体ABCD﹣A1B1C1D1中,E,F分别是AD,DD1的中点,AB=4,则过B,E,F的平面截该正方体所得的截面周长为( )
A.6 ![]() +4
+4 ![]()
B.6 ![]() +2
+2 ![]()
C.3 ![]() +4
+4 ![]()
D.3 ![]() +2
+2 ![]()
【答案】A
【解析】解:∵正方体ABCD﹣A1B1C1D1中,E、F分别是棱AD、DD1的中点, ∴EF∥AD1∥BC1 ,
∵EF平面BCC1 , BC1平面BCC1 ,
∴EF∥平面BCC1 ,
由线面平行性质定理,过EF且过B的平面与面BCC1的交线l平行于EF,l即为BC1 .
由正方体的边长为4,可得截面是以BE=C1F=2 ![]() 为腰,EF=2
为腰,EF=2 ![]() 为上底,BC1=2EF=4
为上底,BC1=2EF=4 ![]() 为下底的等腰梯形,故周长为6
为下底的等腰梯形,故周长为6 ![]() +4
+4 ![]() ,
,
故选A.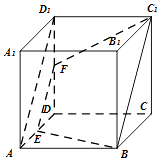
【考点精析】通过灵活运用平面的基本性质及推论,掌握如果一条直线上的两点在一个平面内,那么这条直线在此平面内;过不在一条直线上的三点,有且只有一个平面;如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线即可以解答此题.

【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如右表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5~7分钟,乙每次解答一道几何题所用的时间在6~8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为 X,求 X的分布列及数学期望 EX. 附表及公式
P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() .
.

