题目内容
12.已知函数f(x)=-cos($\frac{x}{2}$-$\frac{π}{3}$).(1)求函数f(x)的单调递增区间.
(2)如何从函数y=cosx的图象变换得到函数y=f(x)的图象?
分析 (1)由条件利用余弦函数的单调性,得出结论.
(2)由条件利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:(1)对于函数f(x)=-cos($\frac{x}{2}$-$\frac{π}{3}$),令2kπ≤$\frac{x}{2}$-$\frac{π}{3}$≤2kπ+π,
求得4kπ+$\frac{2π}{3}$≤x≤4kπ+$\frac{8π}{3}$,故函数f(x)的单调递增区间为[4kπ+$\frac{2π}{3}$,4kπ+$\frac{8π}{3}$],k∈Z.
(2)把函数y=cosx的图象向右平移$\frac{π}{3}$个单位,可得y=cos(x-$\frac{π}{3}$)的图象;
再把所得图象上点的横坐标变为原来的2倍,可得y=cos($\frac{1}{2}$x-$\frac{π}{3}$)的图象;
再把所得图象关于x轴对称,即得函数f(x)=-cos($\frac{x}{2}$-$\frac{π}{3}$)的图象.
点评 本题主要考查余弦函数的单调性,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
2.已知集合A={x|x2-2x-3<0},则A=( )
| A. | {x|x>1} | B. | {x|-1<x<3} | C. | {x|1<x<3} | D. | {x|-1<x<1} |
20.若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为单位向量,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,则|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|的最大值是( )
| A. | 1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{2}$-1 | D. | $\sqrt{2}$ |
17.设a∈R,函数f(x)=x|x-a|-a,若对任意的x∈[2,3],f(x)≥0恒成立,则( )
| A. | a≤1或a≥$\frac{9}{2}$ | B. | a≤$\frac{4}{3}$或a≥$\frac{7}{2}$ | C. | a≤1或a≥$\frac{7}{2}$ | D. | a≤$\frac{4}{3}$或a≥$\frac{9}{2}$ |
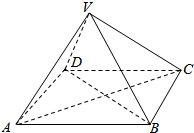 如图,已知四棱锥V-ABCD中,四边形ABCD为正方形,VA=VB=VC=CD,若AB=2,VC=2.
如图,已知四棱锥V-ABCD中,四边形ABCD为正方形,VA=VB=VC=CD,若AB=2,VC=2.