题目内容
已知直线l:3x+4y-12=0与圆C: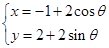 (θ为参数)的位置关系是( )
(θ为参数)的位置关系是( )
| A.相切 | B.相离 | C.相交但直线不过圆心 | D.直线过圆心 |
C
解析试题分析:因为直线l:3x+4y-12=0,而圆C: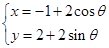 ,消去参数后得到关于x,y的关系式为
,消去参数后得到关于x,y的关系式为 ,故可知圆心坐标为(-1,2),半径为2的圆,因此利用点到直线的距离公式可知,d=
,故可知圆心坐标为(-1,2),半径为2的圆,因此利用点到直线的距离公式可知,d= ,故可知直线l:3x+4y-12=0与圆C:
,故可知直线l:3x+4y-12=0与圆C: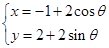 (θ为参数)的位置关系是相交但直线不过圆心,故选C.
(θ为参数)的位置关系是相交但直线不过圆心,故选C.
考点:本题主要考查直线与圆的位置关系的运用。
点评:解决该试题的关键是确定出圆心坐标和圆心到直线的距离公式,比较d与r的关系可知其位置关系,如果d=r,则说明相切,如果d<r,说明是相交,如果是d>r,则说明是相离。

练习册系列答案
相关题目
已知集合 ,
,


 。若存在实数
。若存在实数 使得
使得 成立,称点
成立,称点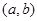 为“£”点,则“£”点在平面区域
为“£”点,则“£”点在平面区域 内的个数是
内的个数是
| A.0 | B.1 | C.2 | D.无数个 |
已知圆 及直线
及直线 当直线
当直线 被圆
被圆 截得的弦长为
截得的弦长为 ,则
,则 ( )
( )
A. | B. | C. | D. |
点 在圆
在圆 内,则直线
内,则直线 和已知圆的公共点个数为
和已知圆的公共点个数为
| A.0 | B.1 | C.2 | D.不能确定 |
设 ,若线段
,若线段 是△
是△ 外接圆的直径,则点
外接圆的直径,则点 的坐标是( ).
的坐标是( ).
| A.(-8,6) | B.(8,-6) | C.(4,-6) | D.(4,-3) |
若直线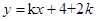 与曲线
与曲线 有两个交点,则
有两个交点,则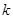 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
圆 :
: 与圆
与圆 公切线的条数是( )
公切线的条数是( )
| A.0条 | B.1条 | C.2条 | D.3条 |
圆 与圆
与圆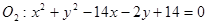 的位置关系是( )
的位置关系是( )
| A.相离 | B.内含 | C.外切 | D.内切 |
直线 与圆
与圆 的位置关系为( )
的位置关系为( )
| A.相切 | B.相交但直线不过圆心 |
| C.直线过圆心 | D.相离 |