题目内容
若直线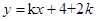 与曲线
与曲线 有两个交点,则
有两个交点,则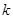 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
D
解析试题分析:由题意可知,作图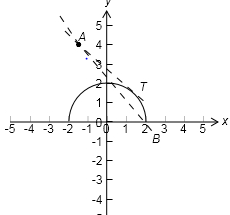
曲线 即x2+y2=4,(y≥0)
即x2+y2=4,(y≥0)
表示一个以(0,0)为圆心,以2为半径的位于x轴上方的半圆,如上图所示:
直线y=kx+4+2k即y=k(x+2)+4,表示恒过点(-2,4)斜率为k的直线,结合图形可得,
kAB=-1,∵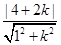 =2解得k=-
=2解得k=-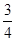 即kAT=-
即kAT=-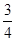
∴要使直线与半圆有两个不同的交点,k的取值范围是[-1,-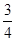 ],故选D
],故选D
考点:本题主要是考查直线与圆的位置关系的运用。
点评:解决该试题的关键是理解直线表示的为过定点(-2,4),斜率为k的直线,而曲线表示的为半个圆,圆心在原点,半径为2的上半个圆,利用数形结合得到结论。

练习册系列答案
相关题目
已知圆的方程为 ,若抛物线过点
,若抛物线过点 ,
, 且以圆的切线为准线,则抛物线的焦点的轨迹方程是
且以圆的切线为准线,则抛物线的焦点的轨迹方程是
A. | B. |
C. | D. |
自点A(3,5)作圆C: 的切线,则切线的方程为( )
的切线,则切线的方程为( )
A. | B. |
C. 或 或 | D.以上都不对 |
已知圆 的圆心为抛物线
的圆心为抛物线 的焦点,且与直线
的焦点,且与直线 相切,则该圆的方程为( )
相切,则该圆的方程为( )
A. | B. |
C. | D. |
已知直线l:3x+4y-12=0与圆C: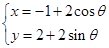 (θ为参数)的位置关系是( )
(θ为参数)的位置关系是( )
| A.相切 | B.相离 | C.相交但直线不过圆心 | D.直线过圆心 |
将圆 平分的直线是( )
平分的直线是( )
A. | B. | C. | D. |
若圆 关于直线
关于直线
 对称,则直线的斜率是( )
对称,则直线的斜率是( )
| A.6 | B. | C. | D.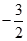 |
若双曲线 的一个焦点是圆
的一个焦点是圆 的圆心,且虚轴长为
的圆心,且虚轴长为 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. |
C. | D. |
已知圆的方程为 .设该圆过点(3,5)的两条弦分别为AC和BD,且
.设该圆过点(3,5)的两条弦分别为AC和BD,且 .则四边形ABCD的面积最大值为( )
.则四边形ABCD的面积最大值为( )
A.20 | B.30 | C.49 | D.50 |