题目内容
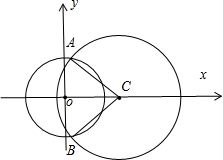
已知两圆x2+y2=9和（x-3）2+y2=27，求大圆被小圆截得劣弧的长度．
由题意，设A(3+3
cosα，3
sinα)，0≤α≤π，
且点A在小圆上
∴(3+3
cosα)2+(3
sinα)2=9
解得cosα=-
∴α=
．
∴∠ACB=
×2=
∴大圆被小圆截得弧长为
×3
=
π
．
| 3 |
| 3 |
且点A在小圆上
∴(3+3
| 3 |
| 3 |
解得cosα=-
| ||
| 2 |
| 5π |
| 6 |
∴∠ACB=
| π |
| 6 |
| π |
| 3 |
∴大圆被小圆截得弧长为
| π |
| 3 |
| 3 |
| 3 |
．
练习册系列答案
相关题目
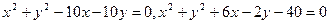，求（1）它们的公共弦所在直线的方程；（2）公共弦长。