题目内容
(12分)设命题p:{x|x2-4ax+3a2<0}(a>0), 
(1)如果a=1,且p∧q为真时,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件时,求实数a的取值范围.
(1)实数x的取值范围是{x|2<x≤3}. (2)实数a的取值范围是{a|1<a≤2}.
解析试题分析:(1)根据题意可知,命题p,q分别表示一元二次不等式的解集,然后利用且命题为真,得到实数x的取值范围。
(2)根据¬p是¬q的充分不必要条件,表明q是p的充分不必要条件,利用集合的思想来求解得到。
(1) 当a>0时, {x|x2-4ax+3a2<0}={x|(x-3a)(x-a)<0}={x|a<x<3a},如果a=1时,则x的取值范围是{x|1<x<3},而{x|x2-x-6≤0,且x2+2x-8>0}={x|2<x≤3},
因为p∧q为真,所以有{x|1<x<3}∩{x|2<x≤3}={x|2<x<3}.故实数x的取值范围是{x|2<x≤3}.
(2) 若¬p是¬q的充分不必要条件,表明q是p的充分不必要条件.由(1)知,{x|2<x≤3}是{x|a<x<3a}(a>0)的真子集,易知a≤2且3<3a,解得{a|1<a≤2}.故实数a的取值范围是{a|1<a≤2}.
考点:本试题主要考查了命题的真值的判定,以及充分条件的判定的运用。
点评:解决该试题的关键是对于命题p,q的正确表示,尤其是含有参数的一元二次不等式不等式的求解,注意根的大小的确定解集,并利用数轴法来得到集合的包含关系进而求解。

练习册系列答案
相关题目
 ,
, ,命题
,命题 ,使得
,使得 .若“
.若“ 或
或 为真”,“
为真”,“ 的取值范围.
的取值范围. 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线 的离心率
的离心率 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。 :实数
:实数 满足
满足 ,其中
,其中 ;命题
;命题 :实数
:实数
 ,且
,且 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.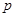 :方程
:方程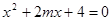 有实数根;命题
有实数根;命题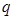 :方程
:方程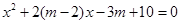 有实数根.已知
有实数根.已知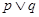 为真,
为真,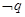 为真,求实数
为真,求实数 的取值范围.
的取值范围. :
: 是减函数,命题
是减函数,命题 :关于
:关于 的不等式
的不等式 的解集为
的解集为 ,如果“
,如果“ 的取值范围.
的取值范围. :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数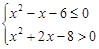 .
. 为真,求实数
为真,求实数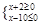 命题q:1-m≤x≤1+m,m>0,
命题q:1-m≤x≤1+m,m>0, ”.
”. 的取值范围.
的取值范围.