题目内容
设命题 :
: 是减函数,命题
是减函数,命题 :关于
:关于 的不等式
的不等式 的解集为
的解集为 ,如果“
,如果“ 或
或 ”为真命题,“
”为真命题,“ 且
且 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.

解析试题分析:若命题 :
: 是减函数真命题,则
是减函数真命题,则 ,
,
若命题 :关于
:关于 的不等式
的不等式 的解集为
的解集为 为真命题,则
为真命题,则 ,则
,则 .
.
又∵“ 或
或 ”为真命题,“
”为真命题,“ 且
且 ”为假命题,则
”为假命题,则 ,
, 恰好一真一假
恰好一真一假
当命题 为真命题,命题
为真命题,命题 为假命题时,
为假命题时,
当命题 为假命题,命题
为假命题,命题 为真命题时,
为真命题时, ,
,
故满足条件的实数 的取值范围是
的取值范围是 .
.
考点:本小题主要考查由复合命题的真假求参数的取值范围,考查了学生分类讨论思想的应用和运算求解能力.
点评:解决此种问题,一般是先求出命题为真时的取值范围,再判断命题的真假,如果命题为假,则取命题为真时的范围的补集即可,这样不大容易出错.

练习册系列答案
相关题目
 :
: ,命题
,命题 :
: ;
; 的取值范围。
的取值范围。 :
: 在
在 上是增函数;命题
上是增函数;命题 函数
函数 存在极大值和极小值。求使命题“
存在极大值和极小值。求使命题“ ”为真命题的
”为真命题的 的取值范围。
的取值范围。
 在区间[-1,1]上单调递减;命题q:函数
在区间[-1,1]上单调递减;命题q:函数 的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围. +2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.
+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围. :关于
:关于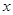 的不等式
的不等式 ,对一切
,对一切 恒成立,命题
恒成立,命题 :函数
:函数 是增函数,若
是增函数,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围.
的取值范围. :对任意
:对任意 ,不等式
,不等式 恒成立;
恒成立; :存在
:存在 ,使不等式
,使不等式 成立,若“
成立,若“ 的取值范围.
的取值范围. :
: ;
;  :
: ,若
,若 是
是 的必要而不充分条件,求实数a的取值范围 。
的必要而不充分条件,求实数a的取值范围 。