[题目]已知数列{an}中.a1＝3.a10＝21.通项an相应的函数是一次函数．(1) 求数列{an}的通项公式,(2) 若{bn}是由a2.a4.a6.a8.-组成.试求数列{bn}的通项公式．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知数列{an}中，a1＝3，a10＝21，通项an相应的函数是一次函数．

(1) 求数列{an}的通项公式；

(2) 若{bn}是由a2，a4，a6，a8，…组成，试求数列{bn}的通项公式．

【答案】（1）an＝2n＋1（2）an＝2n＋14n＋1

【解析】试题分析：（1）一次函数对应解析式为an＝kn＋b，再利用待定系数法求k,b即得数列{an}的通项公式；（2）{bn}是由{an}的偶数项组成,即bn＝a2n，代入即得数列{bn}的通项公式．

试题解析：解：(1) 设an＝kn＋b，由a1＝3，a10＝21，得

解得∴ an＝2n＋1(n∈N*)．

(2) ∵ {bn}是由{an}的偶数项组成，

∴ an＝2n＋1, bn＝a2n＝2×2n＋1＝4n＋1(n∈N*)．

练习册系列答案

相关题目

【题目】集合A是由且备下列性质的函数组成的：

①函数的定义域是；②函数的值域是；

③函数在上是增函数，试分别探究下列两小题：

（1）判断函数数及是否属于集合A？并简要说明理由；

（2）对于（1）中你认为属于集合A的函数，不等式

是否对于任意的恒成立？若成立，请给出证明；若不成立，请说明理由。

【题目】设函数，，且函数的图象关于直线对称。

(1)求函数在区间上最大值；

(2)设，不等式在上恒成立，求实数的取值范围；

(3)设有唯一零点，求实数的值。

【题目】已知函数f(x)＝x2－2|x|－1，－3≤x≤3.

(1)证明：f(x)是偶函数；

(2)指出函数f(x)的单调区间；

(3)求函数的值域.

【题目】已知函数f(x)＝x2－1，g(x)＝

(1)求f[g(2)]和g[f(2)]的值；

(2)求f[g(x)]和g[f(x)]的表达式．

【题目】已知函数（, 是自然对数的底数）.

（1）当时，求曲线在点处的切线方程；

（2）当时，不等式恒成立，求实数的取值范围.

【题目】（本小题满分12分）

甲乙两个班级进行一门课程的考试，按照学生考试成绩优秀和不优秀统计成绩后，得到如下的列联表：

班级与成绩列联表

	优秀	不优秀
甲班	10	35
乙班	7	38

根据列联表的独立性检验，能否在犯错误的概率不超过0.01的前提下认为成绩与班级有关系？

附：

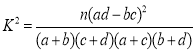
	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

【题目】类比平面内正三角形的“三边相等，三内角相等”的性质，可推出正四面体的下列一些性质，你认为比较恰当的是（）

①各棱长相等，同一顶点上的任两条棱的夹角都相等；②各个面都是全等的正三角形，相邻两个面所成的二面角都相等；③各个面都是全等的正三角形，同一顶点上的任两条棱的夹角都相等。

A. ① B. ②③ C. ①② D. ①②③

【题目】已知函数，其中

（1）当时，求函数在处的切线方程；

（2）若函数在定义域上有且只有一个极值点，求实数的取值范围；

（3）若对任意恒成立，求实数的取值范围.

试题分类