题目内容
【题目】己知圆![]() :
:![]() 和抛物线
和抛物线![]() :
:![]() ,圆
,圆![]() 的切线
的切线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)当直线![]() 的斜率为1时,求
的斜率为1时,求![]() ;
;
(2)设点![]() 为点
为点![]() 关于直线
关于直线![]() 的对称点,是否存在直线
的对称点,是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]()
【解析】
(1)设直线方程为![]() ,根据相切得到
,根据相切得到![]() ,联立方程得到
,联立方程得到![]() ,
,![]() ,根据弦长公式计算得到答案.
,根据弦长公式计算得到答案.
(2)考虑斜率存在和不存在两种情况,联立方程得到![]() ,
,![]() ,根据
,根据![]() ,计算得到答案.
,计算得到答案.
(1)设直线方程为![]() ,则
,则![]() ,故
,故![]() 或
或![]() .
.
当![]() 时,
时,![]() ,无解,舍去;
,无解,舍去;
当![]() 时,
时,![]() ,
,![]() ,故
,故![]() ,
,![]() ,
,![]() .
.
![]() .
.
(2)![]() ,故
,故![]() ,设直线方程为
,设直线方程为![]() ,易知
,易知![]() 时不成立,
时不成立,
设![]() ,
,![]() ,则
,则![]() ,即
,即![]() .
.
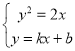 ,故
,故![]() ,
,![]() ,即
,即![]() ,
,
![]() ,
,![]() .
.
![]() ,故
,故![]() ,
,
即![]() ,相减得到
,相减得到![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ,验证满足
,验证满足![]() ,成立;
,成立;
当![]() 时,代入
时,代入![]() 计算得到
计算得到![]() ,无解;
,无解;
当斜率不存在时,直线方程为![]() ,故
,故![]() .
.
此时![]() ,不满足;
,不满足;
综上所述:存在直线![]() ,满足条件.
,满足条件.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目