题目内容
【题目】数列{an}的各项均为正数,且an+1=an+ ![]() ﹣1(n∈N*),{an}的前n项和是Sn .
﹣1(n∈N*),{an}的前n项和是Sn .
(Ⅰ)若{an}是递增数列,求a1的取值范围;
(Ⅱ)若a1>2,且对任意n∈N* , 都有Sn≥na1﹣ ![]() (n﹣1),证明:Sn<2n+1.
(n﹣1),证明:Sn<2n+1.
【答案】解:(Ⅰ)解:由a2>a1>0 ![]() ﹣1>a1>0,解得0<a1<2,①.
﹣1>a1>0,解得0<a1<2,①.
又a3>a2>0, ![]() >a2,0<a2<2
>a2,0<a2<2 ![]() ﹣1<2,解得1<a1<2,②.
﹣1<2,解得1<a1<2,②.
由①②可得:1<a1<2.
下面利用数学归纳法证明:当1<a1<2时,n∈N*,1<an<2成立.
(i)当n=1时,1<a1<2成立.
(ii)假设当n=k∈N*时,1<an<2成立.
则当n=k+1时,ak+1=ak+ ![]() ﹣1∈
﹣1∈ ![]() (1,2),
(1,2),
即n=k+1时,不等式成立.
综上(1)(2)可得:n∈N*,1<an<2成立.
于是an+1﹣an= ![]() ﹣1>0,即an+1>an,
﹣1>0,即an+1>an,
∴{an}是递增数列,a1的取值范围是(1,2).
(Ⅱ)证明:∵a1>2,可用数学归纳法证明:an>2对n∈N*都成立.
于是:an+1﹣an= ![]() ﹣1<2,即数列{an}是递减数列.
﹣1<2,即数列{an}是递减数列.
在Sn≥na1﹣ ![]() (n﹣1)中,令n=2,可得:2a1+
(n﹣1)中,令n=2,可得:2a1+ ![]() ﹣1=S2≥2a1﹣
﹣1=S2≥2a1﹣ ![]() ,解得a1≤3,因此2<a1≤3.
,解得a1≤3,因此2<a1≤3.
下证:(1)当 ![]() 时,Sn≥na1﹣
时,Sn≥na1﹣ ![]() (n﹣1)恒成立.
(n﹣1)恒成立.
事实上,当 ![]() 时,由an=a1+(an﹣a1)≥a1+(2﹣
时,由an=a1+(an﹣a1)≥a1+(2﹣ ![]() )=
)= ![]() .
.
于是Sn=a1+a2+…+an≥a1+(n﹣1) ![]() =na1﹣
=na1﹣ ![]() .
.
再证明:(2) ![]() 时不合题意.
时不合题意.
事实上,当 ![]() 时,设an=bn+2,可得
时,设an=bn+2,可得 ![]() ≤1.
≤1.
由an+1=an+ ![]() ﹣1(n∈N*),可得:bn+1=bn+
﹣1(n∈N*),可得:bn+1=bn+ ![]() ﹣1,可得
﹣1,可得 ![]() =
= ![]() ≤
≤ ![]() ≤
≤ ![]() .
.
于是数列{bn}的前n和Tn≤ 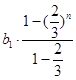 <3b1≤3.
<3b1≤3.
故Sn=2n+Tn<2n+3=na1+(2﹣a1)n+3,③.
令a1= ![]() +t(t>0),由③可得:Sn<na1+(2﹣a1)n+3=na1﹣
+t(t>0),由③可得:Sn<na1+(2﹣a1)n+3=na1﹣ ![]() ﹣tn+
﹣tn+ ![]() .
.
只要n充分大,可得:Sn<na1﹣ ![]() .这与Sn≥na1﹣
.这与Sn≥na1﹣ ![]() (n﹣1)恒成立矛盾.
(n﹣1)恒成立矛盾.
∴ ![]() 时不合题意.
时不合题意.
综上(1)(2)可得: ![]() ,于是可得
,于是可得 ![]() =
= ![]() ≤
≤ ![]() ≤
≤ ![]() .(由
.(由 ![]() 可得:
可得: ![]() ).
).
故数列{bn}的前n项和Tn≤ 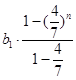 <
< ![]() b1<1,∴Sn=2n+Tn<2n+1
b1<1,∴Sn=2n+Tn<2n+1
【解析】(Ⅰ)由a2>a1>0 ![]() ﹣1>a1>0,解得0<a1<2.又a3>a2>0,
﹣1>a1>0,解得0<a1<2.又a3>a2>0, ![]() >a2,0<a2<2
>a2,0<a2<2 ![]() ﹣1<2,解得1<a1<2.可得:1<a1<2.下面利用数学归纳法证明:当1<a1<2时,n∈N*,1<an<2成立即可.于是an+1﹣an=
﹣1<2,解得1<a1<2.可得:1<a1<2.下面利用数学归纳法证明:当1<a1<2时,n∈N*,1<an<2成立即可.于是an+1﹣an= ![]() ﹣1>0,即an+1>an,满足{an}是递增数列,即可得出a1的取值范围.(Ⅱ)a1>2,可用数学归纳法证明:an>2对n∈N*都成立.于是:an+1﹣an=
﹣1>0,即an+1>an,满足{an}是递增数列,即可得出a1的取值范围.(Ⅱ)a1>2,可用数学归纳法证明:an>2对n∈N*都成立.于是:an+1﹣an= ![]() ﹣1<2,即数列{an}是递减数列.在Sn≥na1﹣
﹣1<2,即数列{an}是递减数列.在Sn≥na1﹣ ![]() (n﹣1)中,令n=2,可得:2a1+
(n﹣1)中,令n=2,可得:2a1+ ![]() ﹣1=S2≥2a1﹣
﹣1=S2≥2a1﹣ ![]() ,解得a1≤3,因此2<a1≤3.
,解得a1≤3,因此2<a1≤3.
下证:(1)当 ![]() 时,Sn≥na1﹣
时,Sn≥na1﹣ ![]() (n﹣1)恒成立.事实上,当
(n﹣1)恒成立.事实上,当 ![]() 时,由an=a1+(an﹣a1)≥a1+(2﹣
时,由an=a1+(an﹣a1)≥a1+(2﹣ ![]() )=
)= ![]() .累加求和即可证明.
.累加求和即可证明.
再证明:(2) ![]() 时不合题意.事实上,当
时不合题意.事实上,当 ![]() 时,设an=bn+2,可得
时,设an=bn+2,可得 ![]() ≤1.由an+1=an+
≤1.由an+1=an+ ![]() ﹣1(n∈N*),可得:bn+1=bn+
﹣1(n∈N*),可得:bn+1=bn+ ![]() ﹣1,可得
﹣1,可得 ![]() =
= ![]() ≤
≤ ![]() ≤
≤ ![]() .于是数列{bn}的前n和Tn≤3.故Sn=2n+Tn<2n+3=na1+(2﹣a1)n+3,令a1=
.于是数列{bn}的前n和Tn≤3.故Sn=2n+Tn<2n+3=na1+(2﹣a1)n+3,令a1= ![]() +t(t>0),可得:Sn<na1﹣
+t(t>0),可得:Sn<na1﹣ ![]() .这与Sn≥na1﹣
.这与Sn≥na1﹣ ![]() (n﹣1)恒成立矛盾.
(n﹣1)恒成立矛盾.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系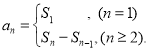 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

【题目】共享单车进驻城市,绿色出行引领时尚,某市有统计数据显示,2016年该市共享单车用户年龄等级分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示,若将共享单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”,使用次数为5次或不足5次的称为“不常使用单车用户”,已知在“经常使用单车用户”中有 ![]() 是“年轻人”.
是“年轻人”. 
(Ⅰ)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列2×2列联表,并根据列联表的独立性检验,判断能有多大把握可以认为经常使用共享单车与年龄有关?
使用共享单车情况与年龄列联表
年轻人 | 非年轻人 | 合计 | |
经常使用共享单车用户 | 120 | ||
不常使用共享单车用户 | 80 | ||
合计 | 160 | 40 | 200 |
(Ⅱ)将频率视为概率,若从该市市民中随机任取3人,设其中经常使用共享单车的“非年轻人”人数为随机变量X,求X的分布列与期望.
(参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
其中,K2= ![]() ,n=a+b+c+d)
,n=a+b+c+d)