题目内容
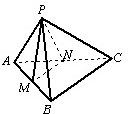
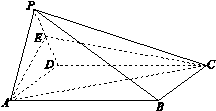
如图,四棱锥P-ABCD中,底面ABCD是边长为6为正方形,PA=PD,
PA⊥平面PDC,E为棱PD的中点.
(Ⅰ)求证:PB∥平面EAC;
(Ⅱ)求证:平面PAD⊥平面ABCD;
(Ⅲ)求四棱锥P-ABCD的体积.
PA⊥平面PDC,E为棱PD的中点.
(Ⅰ)求证:PB∥平面EAC;
(Ⅱ)求证:平面PAD⊥平面ABCD;
(Ⅲ)求四棱锥P-ABCD的体积.

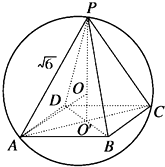
(Ⅰ)证明:连接BD与AC相交于点O,连接EO.
∵四边形ABCD为正方形,∴O为BD中点.
∵E为棱PD的中点,∴PB∥EO.
∵PB?平面EAC,EO?平面EAC,
∴PB∥平面EAC.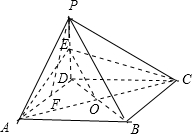
(Ⅱ)证明:PA⊥平面PDC,∴PA⊥CD.
∵四边形ABCD为正方形,∴AD⊥CD,
∴CD⊥平面PAD.
∴平面PAD⊥平面ABCD.
(Ⅲ)取AD中点F,连接PF,∵PA=PD,∴PF⊥AD.
∵平面PAD⊥平面ABCD,∴PF⊥平面ABCD,
又∵PA⊥平面PDC,∴PA⊥PD,∴△PAD为等腰直角三角形.
∵AD=6,∴PF=3.
∴VP-ABCD=
AB•AD•PF=
×6×6×3=36.
∵四边形ABCD为正方形,∴O为BD中点.
∵E为棱PD的中点,∴PB∥EO.
∵PB?平面EAC,EO?平面EAC,
∴PB∥平面EAC.

(Ⅱ)证明:PA⊥平面PDC,∴PA⊥CD.
∵四边形ABCD为正方形,∴AD⊥CD,
∴CD⊥平面PAD.
∴平面PAD⊥平面ABCD.
(Ⅲ)取AD中点F,连接PF,∵PA=PD,∴PF⊥AD.
∵平面PAD⊥平面ABCD,∴PF⊥平面ABCD,
又∵PA⊥平面PDC,∴PA⊥PD,∴△PAD为等腰直角三角形.
∵AD=6,∴PF=3.
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目