题目内容
已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.
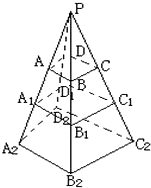

设A1B1C1D1是棱台ABCD-A2B2C2D2的中截面,延长各侧棱交于P点.
∵BC=a,B2C2=b∴B1C1=
∵BC∥B1C1∴
=
∴S△PB1C1=
•S△PBC
同理S△PB2C2=
•S△PBC
∴
=
=
=
=
=
同理:
=
=
=
由等比定理,得
=
故中截面把此棱台侧面分成的两部分面积之比为:
=
.
∵BC=a,B2C2=b∴B1C1=
| a+b |
| 2 |
| S△PBC |
| S△PB1C1 |
| a2 | ||
(
|
∴S△PB1C1=
| (a+b)2 |
| 4a2 |
同理S△PB2C2=
| b2 |
| a2 |
∴
| SB1C1CB |
| SB2C2C1B1 |
| S△PB1C1=S△PBC |
| S△PB2C2-S△PB1C1 |
| ||||
|
| b2+2ab-3a2 |
| 3b2-2ab-a2 |
| (b+3a)(b-a) |
| (3b+a)(b-a) |
| b+3a |
| 3b+a |
同理:
| SABB1A1 |
| SA1B1B2A1 |
| SDCC1D1 |
| SD1C1C2D2 |
| SADD1A1 |
| SA1D1D2A1 |
| b+3a |
| 3b+a |
由等比定理,得
| S上棱台侧 |
| S下棱台侧 |
| 3a+b |
| a+3b |
故中截面把此棱台侧面分成的两部分面积之比为:
| S上棱台侧 |
| S下棱台侧 |
| 3a+b |
| a+3b |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,
,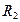 ,
,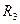 满足
满足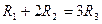 ,则它们的表面积
,则它们的表面积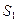 ,
,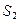 ,
,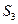 ,满足的等量关系是___________.
,满足的等量关系是___________.