题目内容
在四面体P-ABC中,PA,PB,PC两两垂直,设PA=PB=PC=a,则点P到平面ABC的距离为________.
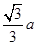
根据题意,可建立如图所示的空间直角坐标系P-xyz,则P(0,0,0),A(a,0,0),B(0,a,0),C(0,0,a).过点P作PH⊥平面ABC,交平面ABC于点H,则PH的长即为点P到平面ABC的距离.

∵PA=PB=PC,∴H为△ABC的外心.
又∵△ABC为正三角形,∴H为△ABC的重心,可得H点的坐标为 .
.
∴PH=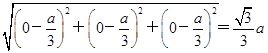 .
.

∵PA=PB=PC,∴H为△ABC的外心.
又∵△ABC为正三角形,∴H为△ABC的重心,可得H点的坐标为
 .
.∴PH=
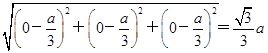 .
.
练习册系列答案
相关题目
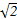 AB,E是SA的中点.
AB,E是SA的中点.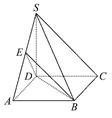
 中,
中, ,底面
,底面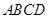 为梯形,
为梯形,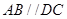 ,
,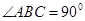 ,且
,且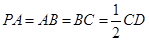 ,
,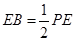 .
.
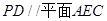 ;
;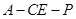 的余弦值.
的余弦值.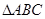 中,
中,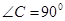 ,
,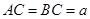 ,点
,点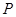 在边
在边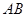 上,设
上,设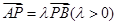 ,过点
,过点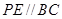 交
交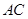 于
于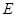 ,作
,作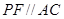 交
交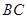 于
于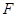 。沿
。沿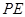 将
将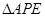 翻折成
翻折成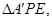 使平面
使平面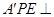 平面
平面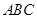 ;沿
;沿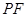 将
将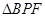 翻折成
翻折成 使平面
使平面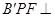 平面
平面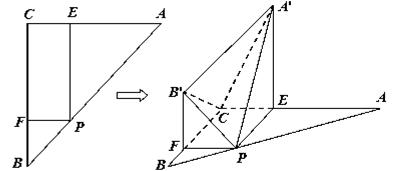
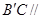 平面
平面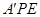 ;
;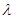 ,使得二面角
,使得二面角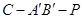 的大小为
的大小为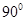 ?若存在,求出
?若存在,求出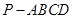 的底面
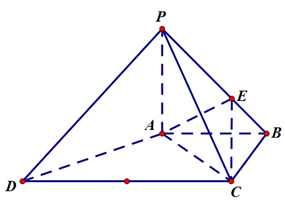
的底面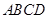 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中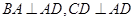 ,
,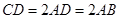 ,平面
,平面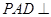 底面
底面 是
是 的中点.
的中点.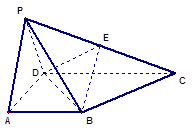
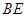 //平面
//平面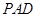 ;
;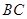 与平面BDE所成角的余弦值;
与平面BDE所成角的余弦值;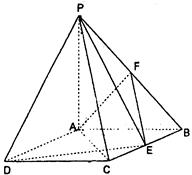
 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.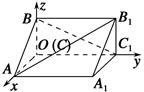
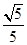
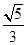
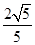
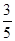
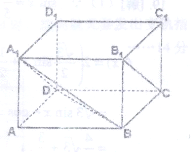
 中,已知DA=DC=4,DD1=3,求异面直线A1B与B1C所成角的余弦值。
中,已知DA=DC=4,DD1=3,求异面直线A1B与B1C所成角的余弦值。