题目内容
【题目】在
中，
，AC，AB边上的中线长之和等于9．
（1）求重心M的轨迹方程；
（2）求顶点A的轨迹方程.
【答案】（1）
1（y≠0）；（2）
1（y≠0）
【解析】
（1）由已知得△ABC重心M在以B、C为两个焦点的椭圆，由此能求出△ABC重心M的轨迹方程．
（2）利用代入法，即可求顶点A的轨迹方程．
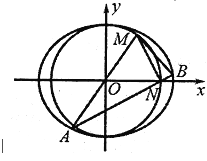
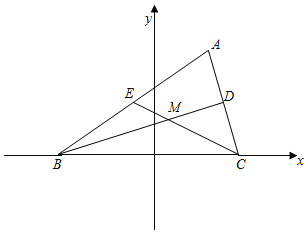
（1）如图所示，以线段BC所在直线为x轴、线段BC的中垂线为y轴建立直角坐标系
设M为△ABC的重心，BD是AC边上的中线，CE是AB边上的中线，由重心的性质知|BM|
|BD|，|CM||CE|，于是|MB|+|MC||BD|
|CE|＝6
根据椭圆的定义知，点M的轨迹是以B、C为焦点的椭圆．2a＝6，2c＝4，
∴a＝3，b
，
故所求的椭圆方程为1（y≠0）
（2）设A（x，y），则M（
x，
），代入1（y≠0），
可得出顶点A的轨迹方程为1（y≠0）
练习册系列答案
阅读快车系列答案
相关题目
