题目内容
【题目】一位同学家里订了一份报纸，送报人每天都在在早上5：20～6：40之间将报纸送到达，该同学的爸爸需要早上6：00～7：00之间出发去上班，则这位同学的爸爸在离开家前能拿到报纸的概率是 ．
【答案】
【解析】解：如图所示， 
设送报人到达的时间为x，这位同学的爸爸在离开家为y；
则（x，y）可以看成平面中的点，试验的全部结果所构成的区域为Ω={（x，y）| 
≤x≤ 
，6≤y≤7}，一个矩形区域，面积为SΩ=1× 
= ，
事件A所构成的区域为A={（x，y）| ≤x≤ ，6≤y≤7，x＜y}即图中的阴影部分，
其中A（6，6），C（ ，6）．B（ ， ），
△ABC面积为= 
× 
× = 
，则阴影部分的面积SA= ﹣ = 
．
则对应的概率P= 
= ．
所以答案是： ．
【考点精析】本题主要考查了几何概型的相关知识点，需要掌握几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等才能正确解答此题．
开心蛙状元测试卷系列答案
【题目】如表是某校120名学生假期阅读时间（单位：小时）的频率分布表，现用分层抽样的方法从[10，15），[15，20），[20，25），[25，30）四组中抽取20名学生了解其阅读内容，那么从这四组中依次抽取的人数是（ ）
分组 | 频数 | 频率 |
[10，15） | 12 | 0，10 |
[15，20） | 30 | a |
[20，25） | m | 0.40 |
[25，30） | n | 0.25 |
合计 | 120 | 1.00 |
A.2，5，8，5
B.2，5，9，4
C.4，10，4，2
D.4，10，3，3
【题目】某位同学在2015年5月进行社会实践活动，为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究，他分别记录了5月1日至5月5日的白天平均气温x（°C）与该奶茶店的这种饮料销量y（杯），得到如下数据：
日 期 | 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 |
平均气温x（°C） | 9 | 10 | 12 | 11 | 8 |
销量y（杯） | 23 | 25 | 30 | 26 | 21 |
（1）若从这五组数据中随机抽出2组，求抽出的2组数据不是相邻2天数据的概率；
（2）请根据所给五组数据，求出y关于x的线性回归方程 
= 
x+ 
．
（参考公式： = 
， = 
﹣ 
）
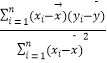