题目内容
18.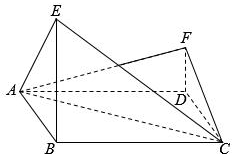 如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面 ABCD,BE=2DF,AE丄EC.(Ⅰ)证明:平面AEC丄平面AFC
(Ⅱ)求直线AE与直线CF所成角的余弦值.
分析 (Ⅰ)连接BD,设BD∩AC=G,连接EG、EF、FG,运用线面垂直的判定定理得到EG⊥平面AFC,再由面面垂直的判定定理,即可得到;
(Ⅱ)以G为坐标原点,分别以GB,GC为x轴,y轴,|GB|为单位长度,建立空间直角坐标系G-xyz,求得A,E,F,C的坐标,运用向量的数量积的定义,计算即可得到所求角的余弦值.
解答 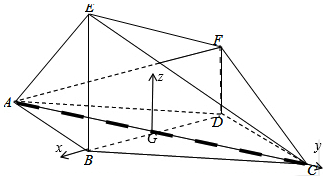 解:(Ⅰ)连接BD,
解:(Ⅰ)连接BD,
设BD∩AC=G,
连接EG、EF、FG,
在菱形ABCD中,
不妨设BG=1,
由∠ABC=120°,
可得AG=GC=$\sqrt{3}$,
BE⊥平面ABCD,AB=BC=2,
可知AE=EC,又AE⊥EC,
所以EG=$\sqrt{3}$,且EG⊥AC,
在直角△EBG中,可得BE=$\sqrt{2}$,故DF=$\frac{\sqrt{2}}{2}$,
在直角三角形FDG中,可得FG=$\frac{\sqrt{6}}{2}$,
在直角梯形BDFE中,由BD=2,BE=$\sqrt{2}$,FD=$\frac{\sqrt{2}}{2}$,可得EF=$\sqrt{{2}^{2}+(\sqrt{2}-\frac{\sqrt{2}}{2})^{2}}$=$\frac{3\sqrt{2}}{2}$,
从而EG2+FG2=EF2,则EG⊥FG,
(或由tan∠EGB•tan∠FGD=$\frac{EB}{BG}$•$\frac{FD}{DG}$=$\sqrt{2}$•$\frac{\sqrt{2}}{2}$=1,
可得∠EGB+∠FGD=90°,则EG⊥FG)
AC∩FG=G,可得EG⊥平面AFC,
由EG?平面AEC,所以平面AEC⊥平面AFC;
(Ⅱ)如图,以G为坐标原点,分别以GB,GC为x轴,y轴,|GB|为单位长度,
建立空间直角坐标系G-xyz,由(Ⅰ)可得A(0,-$\sqrt{3}$,0),E(1,0,$\sqrt{2}$),
F(-1,0,$\frac{\sqrt{2}}{2}$),C(0,$\sqrt{3}$,0),
即有$\overrightarrow{AE}$=(1,$\sqrt{3}$,$\sqrt{2}$),$\overrightarrow{CF}$=(-1,-$\sqrt{3}$,$\frac{\sqrt{2}}{2}$),
故cos<$\overrightarrow{AE}$,$\overrightarrow{CF}$>=$\frac{\overrightarrow{AE}•\overrightarrow{CF}}{|\overrightarrow{AE}|•|\overrightarrow{CF}|}$=$\frac{-1-3+1}{\sqrt{6}×\sqrt{\frac{9}{2}}}$=-$\frac{\sqrt{3}}{3}$.
则有直线AE与直线CF所成角的余弦值为$\frac{\sqrt{3}}{3}$.
点评 本题考查空间直线和平面的位置关系和空间角的求法,主要考查面面垂直的判定定理和异面直线所成的角的求法:向量法,考查运算能力,属于中档题.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{20}$ |
| A. | (-1,0) | B. | (1,0) | C. | (0,-1) | D. | (0,1) |
 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=$\frac{π}{2}$,PA=AD=2,AB=BC=1.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=$\frac{π}{2}$,PA=AD=2,AB=BC=1. 如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.
如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.