题目内容

15．已知集合A={1，2，3}，B={2，3}，则（　　）
A．A=BB．A∩B=∅C．A$\stackrel{?}{≠}$BD．B$\stackrel{?}{≠}$A

分析 直接利用集合的运算法则求解即可．

解答 解：集合A={1，2，3}，B={2，3}，
可得A≠B，A∩B={2，3}，B$\stackrel{?}{≠}$A，所以D正确．
故选：D．

点评 本题考查集合的基本运算，基本知识的考查．

练习册系列答案
相关题目
5．从1，2，3，4，5中有放回的依次取出两个数，则下列各对事件中是互斥事件的是（　　）
A．恰有1个是奇数和全是奇数B．恰有1个是偶数和至少有1个是偶数
C．至少有1个是奇数和全是奇数D．至少有1个是偶数和全是偶数
6．如果3个正整数可作为一个直角三角形三条边的边长，则称这3个数为一组勾股数．从1，2，3，4，5中任取3个不同的数，则这3个数构成一组勾股数的概率为（　　）
A．$\frac{3}{10}$B．$\frac{1}{5}$C．$\frac{1}{10}$D．$\frac{1}{20}$
3．a为实数，函数f（x）=|x2-ax|在区间[0，1]上的最大值记为g（a）．当a=2$\sqrt{2}$-2时，g（a）的值最小．
10．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点为F（-c，0），离心率为$\frac{{\sqrt{3}}}{3}$，点M在椭圆上且位于第一象限，直线FM被圆x2+y2=$\frac{b^2}{4}$截得的线段的长为c，|FM|=$\frac{{4\sqrt{3}}}{3}$．
（Ⅰ）求直线FM的斜率；
（Ⅱ）求椭圆的方程；
（Ⅲ）设动点P在椭圆上，若直线FP的斜率大于$\sqrt{2}$，求直线OP（O为原点）的斜率的取值范围．
20．执行如图所示的程序框图，若输出k的值为8，则判断框图可填入的条件是（　　）
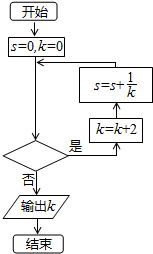
A．s≤$\frac{3}{4}$B．s≤$\frac{5}{6}$C．s≤$\frac{11}{12}$D．s≤$\frac{25}{24}$
7．已知直线l的参数方程为$\left\{{\begin{array}{l}{x=-1+t}\\{y=1+t}\end{array}}$（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为${ρ^2}cos2θ=4（ρ＞0，\frac{3π}{4}＜θ＜\frac{5π}{4}）$，则直线l与曲线C的交点的极坐标为（2，π）．
4．复数（1+2i）i的实部为-2．
5．设$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（1，1），$\overrightarrow{c}$=$\overrightarrow{a}$+k$\overrightarrow{b}$，若$\overrightarrow{b}⊥\overrightarrow{c}$，则实数k的值等于（　　）
A．-$\frac{3}{2}$B．-$\frac{5}{3}$C．$\frac{5}{3}$D．$\frac{3}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网