题目内容
17.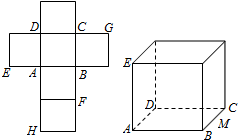 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.(Ⅰ)请将字母F、G、H标记在正方体相应的顶点处(不需说明理由);
(Ⅱ)证明:直线MN∥平面BDH;
(Ⅲ)求二面角A-EG-M的余弦值.
分析 (Ⅰ)根据展开图和直观图之间的关系进行判断即可;
(Ⅱ)利用线面平行的判定定理即可证明直线MN∥平面BDH;
(Ⅲ)法一:利用定义法求出二面角的平面角进行求解.
法二:建立坐标系,利用向量法进行求解即可.
解答 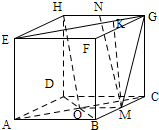 解:(Ⅰ)F、G、H的位置如图;
解:(Ⅰ)F、G、H的位置如图;
证明:(Ⅱ)连接BD,设O是BD的中点,
∵BC的中点为M、GH的中点为N,
∴OM∥CD,OM=$\frac{1}{2}$CD,
HN∥CD,HN=$\frac{1}{2}$CD,
∴OM∥HN,OM=HN,
即四边形MNHO是平行四边形,
∴MN∥OH,
∵MN?平面BDH;OH?面BDH,
∴直线MN∥平面BDH;
(Ⅲ)方法一:
连接AC,过M作MH⊥AC于P,
则正方体ABCD-EFGH中,AC∥EG,
∴MP⊥EG,
过P作PK⊥EG于K,连接KM,
∴EG⊥平面PKM
则KM⊥EG,
则∠PKM是二面角A-EG-M的平面角,
设AD=2,则CM=1,PK=2,
在Rt△CMP中,PM=CMsin45°=$\frac{\sqrt{2}}{2}$,
在Rt△PKM中,KM=$\sqrt{P{K}^{2}+P{M}^{2}}$=$\frac{3\sqrt{2}}{2}$,
∴cos∠PKM=$\frac{PK}{KM}=\frac{2\sqrt{2}}{3}$,
即二面角A-EG-M的余弦值为$\frac{2\sqrt{2}}{3}$.
方法二:以D为坐标原点,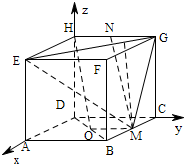
分别为DA,DC,DH方向为x,y,z轴建立空间坐标系如图:
设AD=2,则M(1,2,0),G(0,2,2),E(2,0,2),O(1,1,0),
则$\overrightarrow{GE}$=(2,-2,0),$\overrightarrow{MG}=(-1,0,2)$,
设平面EGM的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{GE}=0}\\{\overrightarrow{n}•\overrightarrow{MG}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2x-2y=0}\\{-x+2z=0}\end{array}\right.$,令x=2,得$\overrightarrow{n}$=(2,2,1),
在正方体中,DO⊥平面AEGC,
则$\overrightarrow{m}$=$\overrightarrow{DO}$=(1,1,0)是平面AEG的一个法向量,
则cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{2+2}{\sqrt{9}×\sqrt{2}}$=$\frac{4}{3\sqrt{2}}$=$\frac{2\sqrt{2}}{3}$.
二面角A-EG-M的余弦值为$\frac{2\sqrt{2}}{3}$.
点评 本题主要考查简单空间图形的直观图,空间线面平行的判定和性质,空间面面夹角的计算,考查空间想象能力,推理能力,运算求解能力.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | 恰有1个是奇数和全是奇数 | B. | 恰有1个是偶数和至少有1个是偶数 | ||
| C. | 至少有1个是奇数和全是奇数 | D. | 至少有1个是偶数和全是偶数 |
| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{20}$ |
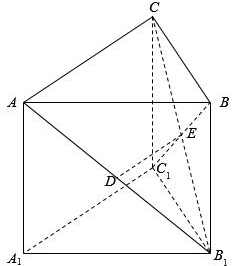 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E. 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=$\frac{π}{2}$,PA=AD=2,AB=BC=1.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=$\frac{π}{2}$,PA=AD=2,AB=BC=1.