题目内容
11.在直角坐标系xOy中,直线C1:x=-2,圆C2:(x-1)2+(y-2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.(Ⅰ)求C1,C2的极坐标方程;
(Ⅱ)若直线C3的极坐标方程为θ=$\frac{π}{4}$(ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.
分析 (Ⅰ)由条件根据x=ρcosθ,y=ρsinθ求得C1,C2的极坐标方程.
(Ⅱ)把直线C3的极坐标方程代入ρ2-3$\sqrt{2}$ρ+4=0,求得ρ1和ρ2的值,结合圆的半径可得C2M⊥C2N,从而求得△C2MN的面积$\frac{1}{2}$•C2M•C2N的值.
解答 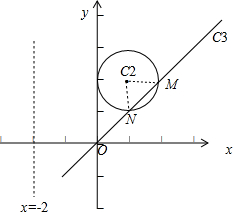 解:(Ⅰ)由于x=ρcosθ,y=ρsinθ,∴C1:x=-2 的
解:(Ⅰ)由于x=ρcosθ,y=ρsinθ,∴C1:x=-2 的
极坐标方程为 ρcosθ=-2,
故C2:(x-1)2+(y-2)2=1的极坐标方程为:
(ρcosθ-1)2+(ρsinθ-2)2=1,
化简可得ρ2-(2ρcosθ+4ρsinθ)+4=0.
(Ⅱ)把直线C3的极坐标方程θ=$\frac{π}{4}$(ρ∈R)代入
圆C2:(x-1)2+(y-2)2=1,
可得ρ2-(2ρcosθ+4ρsinθ)+4=0,
求得ρ1=2$\sqrt{2}$,ρ2=$\sqrt{2}$,
∴|MN|=|ρ1-ρ2|=$\sqrt{2}$,由于圆C2的半径为1,∴C2M⊥C2N,
△C2MN的面积为$\frac{1}{2}$•C2M•C2N=$\frac{1}{2}$•1•1=$\frac{1}{2}$.
点评 本题主要考查简单曲线的极坐标方程,点的极坐标的定义,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
19.设A,B是有限集,定义:d(A,B)=card(A∪B)-card(A∩B),其中card(A)表示有限集A中的元素个数( )
命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;
命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C)
命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件;
命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C)
| A. | 命题①和命题②都成立 | B. | 命题①和命题②都不成立 | ||
| C. | 命题①成立,命题②不成立 | D. | 命题①不成立,命题②成立 |
19.根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )


| A. | 逐年比较,2008年减少二氧化硫排放量的效果最显著 | |
| B. | 2007年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
6.如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数.从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{20}$ |
16.设函数f(x)=ex(2x-1)-ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是( )
| A. | [$-\frac{3}{2e},1$) | B. | [$-\frac{3}{2e},\frac{3}{4}$) | C. | [$\frac{3}{2e},\frac{3}{4}$) | D. | [$\frac{3}{2e},1$) |
20.执行如图所示的程序框图,若输出k的值为8,则判断框图可填入的条件是( )


| A. | s≤$\frac{3}{4}$ | B. | s≤$\frac{5}{6}$ | C. | s≤$\frac{11}{12}$ | D. | s≤$\frac{25}{24}$ |
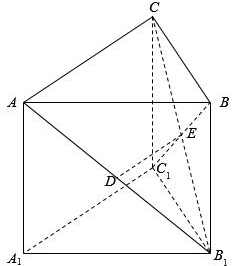 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.