题目内容
已知椭圆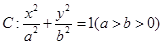 的离心率为
的离心率为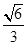 ,焦点到相应准线的距离为
,焦点到相应准线的距离为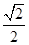
(1)求椭圆C的方程
(2)设直线与椭圆C交于A、B两点,坐标原点到直线的距离为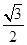 ,求
,求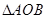 面积的最大值。
面积的最大值。
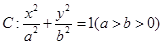 的离心率为
的离心率为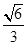 ,焦点到相应准线的距离为
,焦点到相应准线的距离为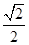
(1)求椭圆C的方程
(2)设直线与椭圆C交于A、B两点,坐标原点到直线的距离为
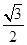 ,求
,求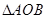 面积的最大值。
面积的最大值。(1)
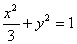
(2)

试题分析:解:(1)
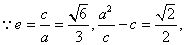 解得
解得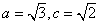
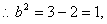 椭圆C的方程为
椭圆C的方程为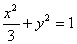
(2)当
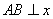 轴时,
轴时,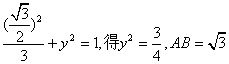 ,
,当AB与x轴不垂直时,设直线l的方程为
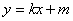 ,
,则

由
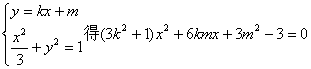
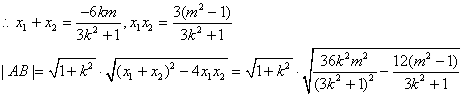
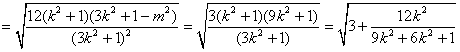
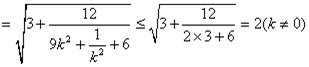 ,
,当且仅当
 ,
,当

 最大时,
最大时,
点评:对于直线与椭圆的位置关系的研究,一般都是联立方程组,结合韦达定理来得到弦长和点到直线距离点到高度,进而求解面积,属于基础题。

练习册系列答案
相关题目
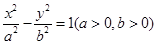 的右焦点
的右焦点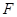 作圆
作圆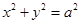 的切线
的切线 (切点为
(切点为 ),交
),交 轴于点
轴于点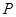 .若
.若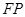 的中点,则双曲线的离心率为
的中点,则双曲线的离心率为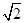
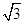
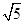
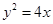 的焦点
的焦点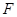 的直线交抛物线于
的直线交抛物线于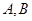 两点,满足
两点,满足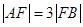 ,则弦
,则弦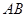 的中点到准线的距离为____.
的中点到准线的距离为____.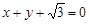 的距离为
的距离为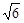 ,离心率
,离心率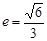
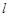 :
: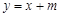 ,是否存在实数m,使直线
,是否存在实数m,使直线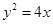 上一点
上一点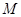 到焦点的距离为3,则点
到焦点的距离为3,则点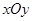 中,以
中,以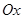 轴为始边作两个锐角
轴为始边作两个锐角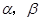 ,它们的终边分别交单位圆于
,它们的终边分别交单位圆于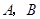 两点.已知
两点.已知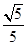 ,
,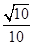 .
.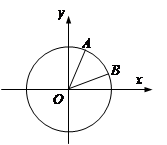
 的值;(2)求
的值;(2)求 的值.
的值.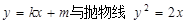 交于A,B两点,且
交于A,B两点,且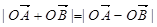 (其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
(其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )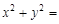 2
2 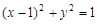
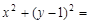 1
1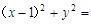 4
4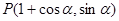 ,参数
,参数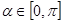 ,点Q在曲线C:
,点Q在曲线C: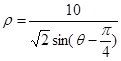 上.
上. 的轨迹方程和曲线C的方程;
的轨迹方程和曲线C的方程;