题目内容
【题目】如图,在三棱锥A﹣BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点. 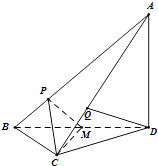
(1)证明:DQ∥平面CPM;
(2)若二面角C﹣AB﹣D的大小为 ![]() ,求∠BDC的正切值.
,求∠BDC的正切值.
【答案】
(1)证明:取AB的中点E,
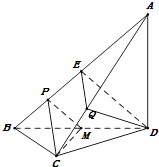
则 ![]() ,所以EQ∥PC.
,所以EQ∥PC.
又EQ平面CPM,所以EQ∥平面CPM.
又PM是△BDE的中位线,所以DE∥PM,
从而DE∥平面CPM.
所以平面DEQ∥平面CPM,
故DQ∥平面CPM.
(2)解法1:由AD⊥平面BCD知,AD⊥CM
由BC=CD,BM=MD,知BD⊥CM,
故CM⊥平面ABD.
由(1)知DE∥PM,而DE⊥AB,故PM⊥AB.
所以∠CPM是二面角C﹣AB﹣D的平面角,
即 ![]() .
.
设PM=a,则 ![]() ,
, ![]() ,
,
在Rt△CMD中, ![]() .
.
所以∠BDC的正切值为 ![]() .
.
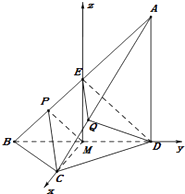
解法2:以M为坐标原点,MC,MD,ME所在的直线分别为x轴,y轴,z轴,
建立如图所示的空间直角坐标系.
设MC=a,MD=b,则C(a,0,0),B(0,﹣b,0),A(0,b,2b)
则 ![]() ,
, ![]()
设 ![]() 平面ABC的一个法向量,
平面ABC的一个法向量,
则 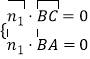 即
即 ![]() 取
取 ![]()
平面ABD的一个法向量为 ![]() ,
,
所以 ![]() ,所以
,所以 ![]()
在Rt△CMD中, ![]()
所以∠BDC的正切值为 ![]() .
.
【解析】(1)取AB的中点E,则EQ∥PC,从而EQ∥平面CPM,由中位线定理得DE∥PM,从而DE∥平面CPM,进而平面DEQ∥平面CPM,由此能证明DQ∥平面CPM.(2)法1:推导出AD⊥CM,BD⊥CM,从而CM⊥平面ABD,进而得到∠CPM是二面角C﹣AB﹣D的平面角,由此能求出∠BDC的正切值.法2:以M为坐标原点,MC,MD,ME所在的直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出∠BDC的正切值.


