题目内容
(2011•临沂二模)在平面直角坐标系中,若不等式组
(a为常数)所表示的平面区域的面积被y轴分成1:2两部分,则a的值为
|
-2或-
| 1 |
| 2 |
-2或-
.| 1 |
| 2 |
分析:如图作出不等式组对应的区域,如图的阴影部分,直线y=ax+1定点C(0,1),根据图形的对称性,故问题转化为求y=ax+1过y轴右侧的A在什么位置时,直线就将阴影部分表示的平面区域的面积被y轴分成1:2两部分.
解答: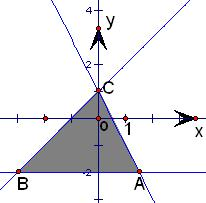 解:易知直线y=ax+1定点C(0,1),作出可行域,
解:易知直线y=ax+1定点C(0,1),作出可行域,
由于B(-3,-2),由图可知,
当直线y=ax+1经过点A(
,-2)或A(6,-2)时,阴影部分表示的平面区域的面积被Y轴分成1:2两部分,
于是直线y=ax+1的斜率:a=kAC=
=-2;或a=kAC=
=-
.
故答案为:-2或-
.
 解:易知直线y=ax+1定点C(0,1),作出可行域,
解:易知直线y=ax+1定点C(0,1),作出可行域,由于B(-3,-2),由图可知,
当直线y=ax+1经过点A(
| 3 |
| 2 |
于是直线y=ax+1的斜率:a=kAC=
| -2-1 | ||
|
| -2-1 |
| 6-0 |
| 1 |
| 2 |
故答案为:-2或-
| 1 |
| 2 |
点评:本题考查线性规划,考查直线与区域的关系,面积公式,训练依据图形进行分析转化的能力,数形结合综合性较强.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 (2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.
(2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R. (2011•临沂二模)如图是某建筑物的三视图,现需将其外部用油漆刷一遍,若每平方米用漆0.1千克,则共需油漆大约为( )(尺寸如图,单位:米,π取3)
(2011•临沂二模)如图是某建筑物的三视图,现需将其外部用油漆刷一遍,若每平方米用漆0.1千克,则共需油漆大约为( )(尺寸如图,单位:米,π取3)