题目内容
【题目】已知等差数列![]() 和等比数列
和等比数列![]() ,其中
,其中![]() 的公差不为0.设
的公差不为0.设![]() 是数列
是数列![]() 的前n项和.若
的前n项和.若![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前3项,且
的前3项,且![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若数列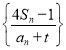 为等差数列,求实数t;
为等差数列,求实数t;
(3)构造数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,….若该数列前n项和
,….若该数列前n项和![]() ,求n的值.
,求n的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)41.
;(3)41.
【解析】
(1)设![]() 的公差
的公差![]() ,由
,由![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前3项,可得
的前3项,可得![]() 即
即![]() ,又
,又![]() 即
即![]() ,解得
,解得![]() ,
,![]() ,即可得出通项公式;
,即可得出通项公式;
(2)![]() ,可得
,可得![]() ,根据数列
,根据数列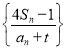 为等差数列,可得
为等差数列,可得![]() ,据此化简求解可得
,据此化简求解可得![]() 值;
值;
(3)设从![]() 到
到![]() 各项的和为
各项的和为![]() ,
,
则![]() ,进而可得
,进而可得 ,由
,由![]() ,
,![]() 得
得![]() ,进而可得该数列前36项的和,令
,进而可得该数列前36项的和,令![]() ,解方程可得
,解方程可得![]() 的值,进而得到
的值,进而得到![]() 的值.
的值.
(1)设![]() 的公差
的公差![]() ,
,![]()
![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前3项,且
的前3项,且![]() ,
,
![]()
![]() ,即
,即![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,公比
,公比![]() ,
,
![]()
![]() ;
;
(2)![]() ,
,
![]()
![]() ,
,
![]() 数列
数列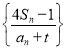 为等差数列,且
为等差数列,且![]() ,
,
![]() 该数列的前三项满足式子:
该数列的前三项满足式子:![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ,经过验证满足题意;
,经过验证满足题意;
(3)由(1)可得:![]() ,数列
,数列![]() 的前n项和
的前n项和![]() ,
,
数列![]() 的前n项和
的前n项和![]() ,
,
设从![]() 到
到![]() 各项的和为
各项的和为![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
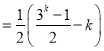 ,
,
![]()
 ,
,
![]()
![]() ,
,![]() ,
,
![]() 取
取![]() ,可得该数列前
,可得该数列前![]() 项的和为
项的和为![]() ,
,
令![]() ,解得
,解得![]() ,
,
因此![]() ,
,
即n的值为41.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目