题目内容

17．某校高一、高二、高三三个年级的学生人数分别为1500人，1200人和1000人，现采用按年级分层抽样法了解学生的视力状况，已知在高二年级抽查了60人，则这次调查三个年级共抽查了多少人？（　　）
A．100B．370C．185D．270

分析 根据高一、高二、高三三个年级的学生数得出总人数，根据高二年级抽查的人数，得出每个个体被抽到的概率，
再用三个年级的总人数乘以概率，即可得出结果．

解答 解：∵高一、高二、高三三个年级的学生数分别为1500人、1200人和1000人，
∴三个年级共有1500+1200+1000=3700（人），
∵高二年级有1200人，高一年级抽查了60人，
∴每个个体被抽到的概率是$\frac{60}{1200}$=$\frac{1}{20}$，
∴三个年级共抽取$\frac{1}{20}$×3700=185（人），
故选：C．

点评 本题考查了分层抽样方法的应用问题，解题的依据是在总体个数，样本容量和每个个体被抽到的概率这三个量中，知二求一，是基础题目．

练习册系列答案
相关题目
1．设数列{an}的前n项$\underset{之}{•}$$\underset{积}{•}$为Tn，且Tn=1-an，（n∈N*）
（I）求a1，并证明数列{$\frac{1}{1-{a}_{n}}$}是等差数列；
（Ⅱ）设Sn=T${\;}_{1}^{2}$+T${\;}_{2}^{2}$+…+T${\;}_{n}^{2}$，求证：$\frac{1}{2}$-$\frac{1}{n+2}$＜Sn＜$\frac{2}{3}$-$\frac{1}{n+2}$（n∈N*）．
8．设集合M={x|y=$\sqrt{1-x}$}，集合N={y|y=x2}，则M∩N=（　　）
A．[0，1）B．[0，1]C．（-∞，1]D．（-∞，1）
5．已知扇形的周长是6cm，面积是2cm2，则扇形的中心角的弧度数是（　　）
A．1B．4C．1或4D．2或4
12．在等差数列{an}和等比数列{bn}中，a1=b1=1，b4=8，{an}的前10项和S10=55．
（1）求数列{an}与{bn}的通项公式；
（2）求数列{anbn}的前n项和Tn．
2．△ABC中，∠A=$\frac{π}{3}$，BC=2$\sqrt{3}$，设∠B为x，周长为y，求：
（1）函数y=f（x）的解析式和定义域；
（2）周长的最大值．
9．在△ABC中，a、b、c分别是角A、B、C的对边，且$\frac{cosB}{cosC}$=-$\frac{b}{2a+c}$．
（1）求角B的大小；
（2）若b=$\sqrt{13}$，a+c=4，求△ABC的面积．
（3）若b=$\sqrt{3}$，求△ABC的面积的最大值．
6．设P，Q分别是圆（x+2）2+（y-7）2=1与抛物线y2=x上的点，则P，Q两点的最小距离为（　　）
A．$\sqrt{73}$B．$\sqrt{73}$-1C．3$\sqrt{5}$D．3$\sqrt{5}$-1
7．如图，四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{DC}$，则必有（　　）
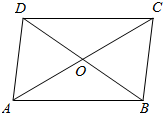
A．$\overrightarrow{AD}$=$\overrightarrow{CB}$B．$\overrightarrow{OA}$=$\overrightarrow{OC}$C．$\overrightarrow{AC}$=$\overrightarrow{DB}$D．$\overrightarrow{DO}$=$\overrightarrow{OB}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网