题目内容

14．如图可能是下列哪个函数的图象（　　）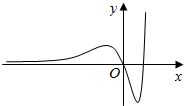
A．y=$\frac{x}{x+1}$B．y=$\frac{x}{lnx}$C．y=（x2-2x）exD．y=x2-2|x|

分析 由题意，x∈R，排除A，B，D是偶函数，即可得出结论．

解答 解：由题意，x∈R，排除A，B，D是偶函数，
故选：C．

点评 本题考查函数的图象，考查数形结合的数学思想，比较基础．

练习册系列答案
相关题目
4．sin2•cos3•tan4小于 0（填大于，小于或等于）．
5．已知扇形的周长是6cm，面积是2cm2，则扇形的中心角的弧度数是（　　）
A．1B．4C．1或4D．2或4
2．△ABC中，∠A=$\frac{π}{3}$，BC=2$\sqrt{3}$，设∠B为x，周长为y，求：
（1）函数y=f（x）的解析式和定义域；
（2）周长的最大值．
9．在△ABC中，a、b、c分别是角A、B、C的对边，且$\frac{cosB}{cosC}$=-$\frac{b}{2a+c}$．
（1）求角B的大小；
（2）若b=$\sqrt{13}$，a+c=4，求△ABC的面积．
（3）若b=$\sqrt{3}$，求△ABC的面积的最大值．
19．设全集U为实数集R，N={x|1＜x＜3}，M={x|x＞2}，则图中阴影部分所表示的集合是（　　）
A．{x|x＜2}B．{x|-2≤x≤2}C．{x|-2≤x＜1}D．{x|1＜x≤2}
6．设P，Q分别是圆（x+2）2+（y-7）2=1与抛物线y2=x上的点，则P，Q两点的最小距离为（　　）
A．$\sqrt{73}$B．$\sqrt{73}$-1C．3$\sqrt{5}$D．3$\sqrt{5}$-1
3．已知a，b，c，d成等比数列，且曲线y=x2-2x+3的顶点坐标为（b，c），则a+d=（　　）
A．3B．$\frac{9}{2}$C．$\frac{5}{2}$D．4
4．函数f（x）=x3+3x2+3ax-4既有极大值又有极小值，则函数g（x）=x+$\frac{a}{x}$-2a在区间（1，+∞）上一定（　　）
A．有最小值B．有最大值C．是减函数D．是增函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网