题目内容
【题目】定义平面向量的一种运算:![]() (
(![]() 是向量
是向量![]() 和
和![]() 的夹角),则下列命题:
的夹角),则下列命题:
①![]() ;②
;②![]() ;③若
;③若![]() 且
且![]() ,则
,则![]() ;其中真命题的序号是___________________.
;其中真命题的序号是___________________.
【答案】①③
【解析】
①由新定义可得![]() 即可判断出;②由新定义可得
即可判断出;②由新定义可得![]() =λ|
=λ|![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >,而(λ
>,而(λ![]() )
)![]() =|λ
=|λ![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >,当λ<0时,
>,当λ<0时,![]() 不成立;③若
不成立;③若![]() ,且λ>0,则
,且λ>0,则![]() =(1+λ)
=(1+λ)![]() ,由新定义可得(
,由新定义可得(![]() )
)![]() =|(1+λ)||
=|(1+λ)|| ![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >,而(
>,而(![]()
![]() )+(
)+(![]()
![]() )=|λ
)=|λ![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >+|
>+| ![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >=|1+λ||
>=|1+λ||![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >.即可判断出.
>.即可判断出.
①由新定义可得![]() ,故恒成立;
,故恒成立;
②由新定义可得![]() =λ|
=λ|![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >,而(λ
>,而(λ![]() )
)![]() =|λ
=|λ![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >,当λ<0时,
>,当λ<0时,![]() 不成立;
不成立;
③若![]() =λ
=λ![]() ,且
,且![]() +
+![]() =(1+λ)
=(1+λ)![]() ,若
,若![]() ,且λ>0,则
,且λ>0,则![]() =(1+λ)
=(1+λ)![]() ,由新定义可得(
,由新定义可得(![]() )
)![]() =|(1+λ)||
=|(1+λ)|| ![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >,而(
>,而(![]()
![]() )+(
)+(![]()
![]() )=|λ
)=|λ![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >+|
>+| ![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >=|1+λ||
>=|1+λ||![]() ||
||![]() |sin<
|sin<![]() ,
,![]() >.
>.![]() 成立.
成立.
综上可知:只有①③恒成立.
故答案为:①③

【题目】企业需为员工缴纳社会保险,缴费标准是根据职工本人上一年度月平均工资(单位:元)的![]() 缴纳,
缴纳,
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企业员工甲在2014年至2018年各年中每月所撒纳的养老保险数额y(单位:元)与年份序号t的统计如下表:
(1)求出t关于t的线性回归方程![]() ;
;
(2)试预测2019年该员工的月平均工资为多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(注: ,
,![]() ,其中
,其中![]() )
)
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(Ⅱ)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销量量不低于10万件的概率.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为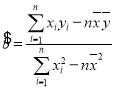 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.