题目内容

【题目】正四面体是侧棱与底面边长都相等的正三棱锥，它的对棱互相垂直.有一个如图所示的正四面体，E，F，G分别是棱AB，BC，CD的中点.

（1）求证：面EFG；

（2）求异面直线EG与AC所成角的大小.

【答案】（1）证明见解析；（2）

【解析】

（1）连接EF，FG，GE，通过三角形的中位线可得，进而可得面EFG；

（2）由题可得为异面直线EG与AC所成角，根据正四棱锥的特点得到为等腰直角三角形，进而可得结果.

解：（1）连接EF，FG，GE，如图，

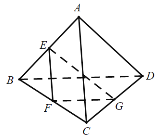
E，F分别是棱AB，BC的中点，

，又面EFG，面EFG，

面EFG；

（2）由（1），则为异面直线EG与AC所成角，

AC与BD是正四面体的对棱，

，又，

，

又 ，

为等腰直角三角形，

，

即异面直线EG与AC所成角的大小为.

练习册系列答案
相关题目

【题目】为了改善市民的生活环境，长沙某大型工业城市决定对长沙市的1万家中小型化工企业进行污染情况摸排，并出台相应的整治措施．通过对这些企业的排污口水质，周边空气质量等的检验，把污染情况综合折算成标准分100分，发现长沙市的这些化工企业污染情况标准分基本服从正态分布N（50，162），分值越低，说明污染越严重；如果分值在［50，60］内，可以认为该企业治污水平基本达标．

（Ⅰ）如图为长沙市的某工业区所有被调査的化工企业的污染情况标准分的频率分布直方图，请计算这个工业区被调査的化工企业的污染情况标准分的平均值，并判断该工业区的化工企业的治污平均值水平是否基本达标；

（Ⅱ）大量调査表明，如果污染企业继续生产，那么标准分低于18分的化工企业每月对周边造成的直接损失约为10万元，标准分在［18，34）内的化工企业每月对周边造成的直接损失约为4万元．长沙市决定关停80％的标准分低于18分的化工企业和60％的标准分在［18，34）内的化工企业，每月可减少的直接损失约有多少？

（附：若随机变量，则， ，）

【题目】已知椭圆

（1）求椭圆的标准方程和离心率；

（2）是否存在过点的直线与椭圆相交于，两点，且满足．若存在，求出直线的方程；若不存在，请说明理由．

【题目】定义平面向量的一种运算：（是向量和的夹角），则下列命题：

①；②；③若且，则；其中真命题的序号是___________________.

【题目】如图所示，在四棱锥中，四边形为矩形， 为等腰三角形， ，平面平面，且， ， 分别为的中点.

（1）证明： 平面；

（2）证明：平面平面；

（3）求四棱锥的体积.

【题目】某市有一面积为12000平方米的三角形地块，其中边长为200米，现计划建一个如图所示的长方形停车场，停车场的四个顶点都在的三条边上，其余的地面全部绿化.若建停车场的费用为180元/平方米，绿化的费用为60元/平方米，设米，建设工程的总费用为元.

（1）求关于的函数表达式：

（2）求停车场面积最大时的值，并求此时的工程总费用.

【题目】等比数列{an}的各项均为正数，且2a1＋3a2＝1， ＝9a2a6.

(1)求数列{an}的通项公式；

(2)设bn＝log3a1＋log3a2＋…＋log3an，求数列的前n项和．

【题目】从，，等8人中选出5人排成一排.

（1）必须在内，有多少种排法？

（2），，三人不全在内，有多少种排法？

（3），，都在内，且，必须相邻，与，都不相邻，都多少种排法？

（4）不允许站排头和排尾，不允许站在中间（第三位），有多少种排法？

【题目】2019年篮球世界杯在中国举行，中国男篮由于主场作战而备受观众瞩目.为了调查国人对中国男篮能否进入十六强持有的态度，调查人员随机抽取了男性观众与女性观众各100名进行调查，所得情况如下表所示：

男性观众

女性观众

认为中国男篮能够进入十六强

60

认为中国男篮不能进入十六强

若在被抽查的200名观众中随机抽取1人，抽到认为中国男篮不能进入十六强的女性观众的概率为.

（1）完善上述表格；

（2）是否有99%的把握认为性别与对中国男篮能否进入十六强持有的态度有关？

附：，其中.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网